Introducción

En la actualidad, Menéndez Cevallos et al. (2024) destacan el creciente interés en comprender los factores que determinan el éxito académico y el logro de un aprendizaje significativo en la formación de profesionales. De acuerdo con Covarrubias Papahiu y Martínez Estrada (2007), se ha llegado a la conclusión de que estos factores están estrechamente relacionados con aspectos emocionales, motivacionales y actitudinales, los cuales desempeñan un papel crucial en los procesos de enseñanza.

Este trabajo se enmarca en el contexto del programa de Administración Pública Territorial (APT) de la Escuela Superior de Administración Pública (ESAP), cuya misión es responder “…a las necesidades del país en cuanto a la generación, difusión y aplicación de conocimiento relacionado con los desafíos de la administración pública, la sociedad y el Estado” (ESAP-PEP, 2021). Por lo tanto, el rechazo, la negación y la frustración que algunos estudiantes experimentan al tratar de recordar y aplicar conceptos matemáticos específicos del programa tienen un impacto directo en el objetivo de formación profesional, que es cultivar la comprensión y la capacidad de resolución de problemas en el ámbito de la administración pública (ESAP, 2022a).

La actitud negativa de los estudiantes hacia las matemáticas, arraigada en emociones negativas como la ansiedad, la frustración, el rechazo, la negación, entre otras, limita su capacidad para desarrollar emociones positivas como la dedicación, el esfuerzo, la curiosidad y la confianza. Estas emociones positivas son fundamentales para determinar el éxito o el fracaso académico (Gómez-Chacón, 2010; Rojas-Kramer et al., 2017). En consecuencia, esta relación actitudinal adversa obstaculiza el desarrollo de habilidades y capacidades esenciales para un administrador público, tales como la planificación, la organización, el estudio, la toma de decisiones, el análisis de casos, la propuesta de soluciones y la elaboración de estrategias de gestión y financiamiento, entre otras responsabilidades gerenciales (ESAP, 2022a).

Desde una edad temprana, las matemáticas suelen percibirse como una materia difícil de comprender y aplicar en la resolución de problemas. Este estigma debe ser superado en la formación de profesionales en administración pública, ya que los fundamentos matemáticos desempeñan un papel vital en el desarrollo de habilidades esenciales, como la jerarquización, la ponderación, la planificación, la medición, la cuantificación y la investigación. Estas habilidades son fundamentales para la toma de decisiones y la gestión pública (Villamizar Herrera et al., 2012).

En este contexto, las reflexiones pedagógicas buscan promover un entendimiento efectivo y una aprehensión significativa para transmitir conocimientos específicos en administración y economía. Además, se busca fomentar la innovación y la creatividad en las herramientas pedagógicas y didácticas necesarias para enseñar conceptos, operaciones, relaciones y propiedades matemáticas. El objetivo es crear un entorno pedagógico que difiera de las metodologías tradicionales y que redefina la actitud de los estudiantes hacia las matemáticas, contribuyendo al desarrollo de competencias propias de cada etapa de su formación (Duque et al., 2013; Evendi et al., 2022).

De esta manera, este artículo propone reflexionar sobre los procesos de enseñanza y aprendizaje de las matemáticas en el contexto de la formación del APT de la ESAP en Colombia, enfocándose en los microcurrículos del programa en el núcleo de formación general, la actitud del alumnado hacia las matemáticas y el aprendizaje basado en problemas (ABP) como estrategia pedagógica. Además, se presenta un ejemplo de cómo la implementación del ABP puede mejorar los procesos de enseñanza y aprendizaje.

Actitud hacia las matemáticas

La actitud puede definirse como una predisposición evaluativa, positiva o negativa, que determina las intenciones de una persona y, por ende, puede influir en su comportamiento. La actitud se compone de tres elementos: un componente cognitivo, manifestado en las creencias; un componente afectivo, que refleja sentimientos de aceptación o rechazo; y un componente intencional, que determina ciertos tipos de conductas en el individuo (Gómez-Chacón, 2010).

Las actitudes hacia las matemáticas se refieren a la valoración, el aprecio y el interés que tiene el sujeto por esta disciplina y su aprendizaje. Este aspecto está más relacionado con el componente afectivo que con el cognitivo, ya que la persona puede manifestar interés, satisfacción, curiosidad, valoración, agrado y motivación, sin que exista una relación directa con su capacidad cognitiva para aprender la disciplina (Gómez-Chacón, 2010).

Se ha observado que una actitud negativa hacia las matemáticas está asociada con los niveles de deserción escolar, tanto en la educación básica como en la superior, y se manifiesta en diversas áreas del conocimiento. Las relaciones frustrantes en el proceso escolar, en ocasiones, se refuerzan o profundizan, lo que se traduce en dificultades personales, emocionales y motivacionales de los estudiantes cuando se enfrentan a esta asignatura (Flores y Auzmendi, 2018; Sattarova et al., 2021).

Esta actitud hacia las matemáticas puede generar cambios en proyectos de vida o, en el peor de los casos, llevar al estancamiento de estos. Sin embargo, es evidente que todas las carreras universitarias requieren el desarrollo de competencias y habilidades de razonamiento y manejo de datos para la resolución de problemas (Abal et al., 2018; Ismail y Imawan, 2022).

Investigaciones sobre la actitud de los estudiantes en programas de Administración hacia las matemáticas sugieren que existen sentimientos negativos hacia la forma en que se enseñan, la prevalencia de exámenes escritos como método de evaluación, las actividades de aprendizaje y la actitud de los profesores en el aula, entre otros aspectos relacionados con la educación (Daza y Garza, 2018; Rocha et al., 2020; Velázquez Rosado et al., 2021). Aunque los estudiantes reconocen la importancia de la asignatura en el ámbito académico y en la vida cotidiana, perciben desconfianza en su aplicación y capacidad requerida, así como un gusto menor por la disciplina (Laverde et al., 2015; Méndez Castro, 2023).

Otro hallazgo significativo indica que la enseñanza de las matemáticas no debe limitarse a presentar fórmulas y a la práctica de ejercicios de aplicación. En su lugar, debería enfocarse en clases inductivas que fomenten la reflexión y el pensamiento crítico, contribuyendo así a la formación de individuos capaces de tomar decisiones informadas en situaciones financieras y cotidianas (Chuquisana Mora, 2015; Evendi et al., 2022).

En un análisis sobre el papel de las matemáticas y la estadística en la Reforma Curricular de la ESAP, presentado por Riascos Villegas (2014), se discute el rol de la enseñanza de las matemáticas en una escuela de administración pública, su relevancia social y los motivos su inclusión en el currículo. A través de una encuesta realizada, entre estudiantes de todas las sedes de la ESAP, sobre la percepción de las matemáticas en la administración pública y su enseñanza, se concluyó que la ESAP ofrece muy pocos cursos cuantitativos en comparación con otros programas de administración pública en Colombia. Esta diferencia se acentúa aún más al compararla con los mejores programas de Administración de Empresas en el país.

Microcurrículos de Administración Pública Territorial en la ESAP

Dentro del diseño curricular por núcleos problemáticos, el microcurrículo aborda el nivel más específico y concreto, correspondiendo a los problemas específicos que conforman un núcleo del plan de estudios. Esto permite abordar adecuadamente el aprendizaje del estudiante, facilitando la reflexión sobre el desarrollo del plan de estudios (Universidad de Antioquia, 1999). En otras palabras, el microcurrículo representa el nivel más preciso de planificación docente y, para su formalización, debe componerse de aspectos integradores, tales como: propósito, evaluación, enseñanza, programación, didáctica y recursos (Manobanda Calberto et al., 2022).

El programa de APT de la ESAP se fundamenta en su Proyecto Educativo del Programa (PEP), cuyo objetivo es proporcionar orientación tanto a la comunidad académica del programa como a las comunidades académicas y científicas a nivel nacional e internacional. Este PEP busca destacar los elementos distintivos que moldean la gestión administrativa, académica y curricular del programa (ESAP-PEP, 2021). Así mismo, el programa contempla siete núcleos temáticos en su plan de estudios: Espacio, Tiempo y Territorio; Gestión del Territorio; Organizaciones Públicas; Problemática Pública; Problemática del Estado y Poder; Economía de lo Público; y Formación General.

El núcleo de Formación General abarca las asignaturas de Matemáticas I, Matemáticas II, Estadística I, Estadística II y Matemática Financiera, cada una con su respectiva Guía Didáctica y/o Microcurrículo, que se considera como el instrumento de planificación académica para la formación del estudiante. Los microcurrículos de estas asignaturas comprenden la estructuración de los contenidos, las estrategias de enseñanza y aprendizaje, los recursos didácticos, los criterios de evaluación y los productos de aprendizaje. Estos aspectos orientan al docente en la planificación de sus clases, favoreciendo la formación cognitiva del estudiante. Es importante destacar que las matemáticas son una ciencia acumulativa y progresiva, donde es necesario aprender los conceptos básicos antes de abordar temas más complejos, adentrándose en sus ideas y expresiones. La lógica matemática y la teoría de conjuntos son fundamentales para comprender cualquier noción matemática.

De igual forma, dentro de los procesos de capacitación docente y acreditación del programa APT, se presentan lineamientos y componentes pedagógicos para el desarrollo de competencias, mencionando el ABP como estrategia de enseñanza y aprendizaje. Estos aspectos están contemplados en el Plan Institucional de Capacitación 2022-2023 (ESAP, 2022a, 2023), así como en los microcurrículos del núcleo de Formación General y el Proceso de Acreditación APT 2016 (ESAP, 2016), como se expone en el Documento de Trabajo #3-Modelos Pedagógicos (Duque Cante, 2021). Sin embargo, no existe una ruta clara para el docente sobre cómo elaborar un ABP específico para la APT. Se considera que el ABP puede ser una respuesta a una formación profesional contextualizada y centrada en el territorio, en las que se integren las competencias, habilidades y conceptos matemáticos necesarios para la toma de decisiones y la gestión pública (Rézio et al., 2022).

Aprendizaje basado en problemas para Administración Pública Territorial

El ABP es una metodología de enseñanza y aprendizaje que se organiza en torno a la investigación de problemas del mundo real. En esta metodología, tanto estudiantes como profesores se involucran en analizar, comprender y proponer soluciones a situaciones diseñadas específicamente para que el estudiante desarrolle determinadas habilidades previstas en el currículo. Estas situaciones o problemas son cuidadosamente diseñados en escenarios que involucran a los estudiantes con hechos de su vida diaria, ya sea en la escuela, en casa o en su ciudad (Castro Martín y Silva Lorente, 2022; Lopes et al., 2019).

Otra definición describe al ABP como un proceso de indagación que resuelve preguntas sobre fenómenos o hechos complejos de la vida. Utiliza un problema definido a partir de cualquier duda, dificultad o incertidumbre, comprendiéndolo desde distintas perspectivas o disciplinas para plantear posibles soluciones. En este proceso, la indagación realizada por el alumno es determinante, ya que resulta en la adquisición de habilidades para resolver problemas de diversa índole (Awaludin et al., 2020; Barell, 2007).

Para el APT, el ABP tiene como objetivo principal que el estudiante adquiera las competencias profesionales y ocupacionales, logre los desempeños o resultados de aprendizaje y cubra los contenidos temáticos definidos en el microcurrículo de cada asignatura. Esto se realiza a través de una situación problema que fomente el análisis, la comprensión y la búsqueda de soluciones mediante el trabajo en equipo (Lavado-Puente et al., 2023).

Esta metodología requiere que los educadores creen un ambiente de aprendizaje adaptado, que facilite el acceso a la información y modele y guíe el proceso (Barco Rojas et al., 2022). Además, entre las responsabilidades de los docentes se incluyen promover la reflexión metacognitiva, apoyar el trabajo en equipo y el esfuerzo individual, identificar problemas, ofrecer soluciones, proporcionar retroalimentación y evaluar los resultados del aprendizaje (Bueno et al., 2004; Chilán Intriago y Párraga Álava, 2023).

Un elemento esencial en la función del educador es asegurarse de que el estudiante asuma su rol y las responsabilidades correspondiente. En el ABP, los estudiantes deben involucrarse de manera activa en un proceso de investigación metódica que requiere la toma de decisiones sobre sus metas de aprendizaje, exploración de temas y construcción de conocimiento de forma autónoma (Padilla Doria y Flórez Nisperuza, 2021). Por esta razón, los entornos de aprendizaje deben fomentar la autonomía para la toma de decisiones y la responsabilidad en el cumplimiento de períodos de trabajo independiente sin supervisión, conocido como trabajo autónomo (Ortiz Diaz y Cutimbo Lozano, 2022; Servicio de Innovación Educativa de la UPM, 2008). Además, los estudiantes deben desarrollar las capacidades necesarias para interactuar con sus compañeros, combinando sus conocimientos y habilidades en un trabajo conjunto para alcanzar objetivos comunes, denominado trabajo colaborativo (Amador Alarcón et al., 2023; León Loaiza y Sánchez, 2023; Lillo Zúñiga, 2013).

Dentro del trabajo colaborativo, los estudiantes deben asumir y asignar roles que les permitan trabajar en conjunto para analizar, comprender y buscar soluciones. Los roles más importantes dentro de un grupo colaborativo pueden ser los siguientes (Barkley et al., 2012):

• Coordinador/Moderador: organiza los pasos que el grupo debe seguir, manteniéndolo enfocado en la tarea asignada. Asigna turnos para que los miembros se expresen en momentos de trabajo colaborativo, como la discusión conjunta, la toma de decisiones y la planificación de tareas. Debe garantizar que todos los miembros del equipo participen de manera equitativa y ordenada, así como brindar apoyo y ánimo a sus compañeros. También debe mostrar aprecio por los logros individuales y del equipo y ejercer liderazgo en el grupo.

• Secretario: registra las decisiones tomadas por el grupo, las respuestas obtenidas y la información relevante. Debe asegurarse de que se utilice un lenguaje apropiado y de mantener un registro de las actividades y progresos del equipo. Suele ser la persona encargada de archivar y guardar el material que se genera durante las sesiones de trabajo en grupo.

• Portavoz: expresa el punto de vista del grupo, ya sea para informar, plantear preguntas o solicitar asistencia. Actúa como representante del equipo al comunicar los resultados de su trabajo al público en general. Este rol puede ser desafiante, ya que implica la capacidad de separarse de las opiniones y experiencias individuales para hablar en nombre de todo el equipo, reflejando el consenso alcanzado y reconociendo las dificultades enfrentadas en la toma de decisiones.

• Encargado del material: adquiere y devuelve los materiales necesarios para el funcionamiento del grupo, supervisando su limpieza y organización después de su uso, garantizando que se devuelvan en perfectas condiciones. Otra de sus tareas incluye recordar a los miembros sobre el compromiso de traer materiales para llevar a cabo el trabajo y asegurar que estos se cumplan.

Por otro lado, el diseño de estos entornos de aprendizaje implica una planificación cuidadosa por parte del docente y requiere tiempo previo a su implementación con los estudiantes. Además, según el número de participantes, se definen las variantes del ABP (Ortiz Ramos, 2020).

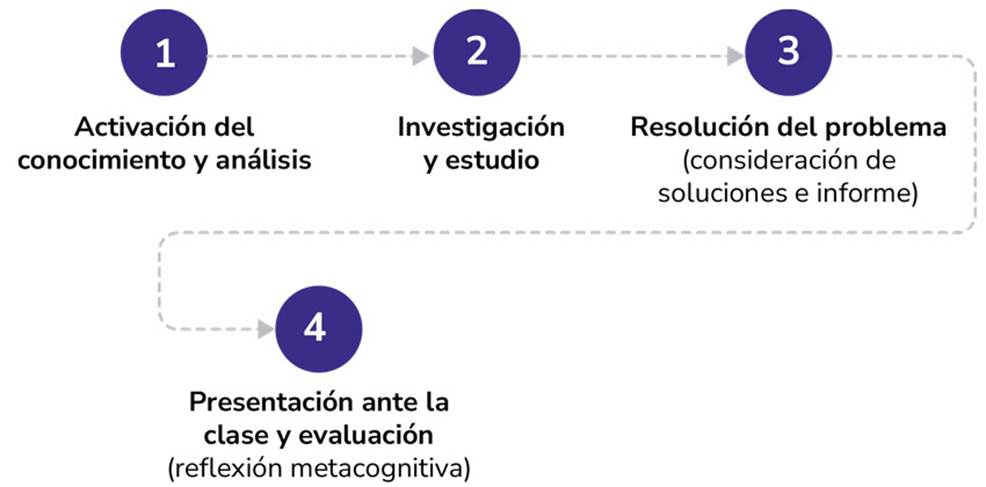
Según Prieto Martín et al. (2006) , la planificación del ABP, según el modelo 4x4, está diseñada para implementarse con más de 100 estudiantes y comprende las siguientes fases (figura 1).

Figura 1: Modelo 4X4.

Fuente: adaptado de Prieto Martín et al. (2006) .

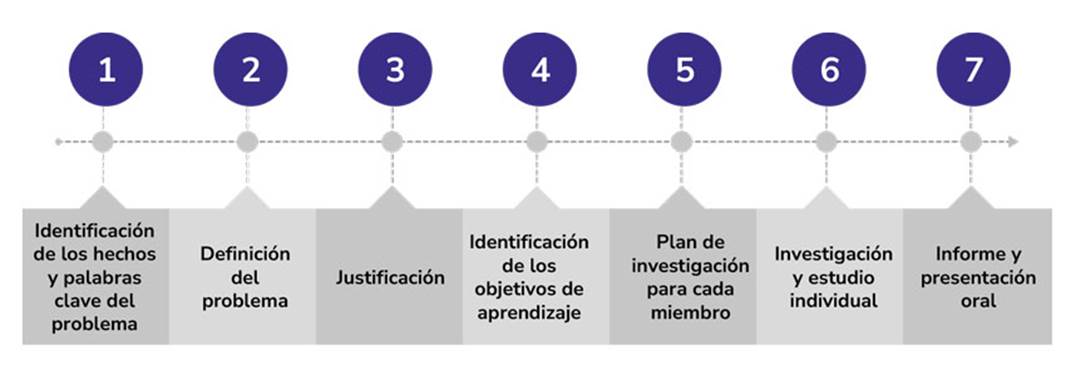
Por su parte, Arpí Miró et al. (2012) indican que la planificación del ABP, según el modelo Hong Kong está diseñada para grupos de entre 50 y 70 estudiantes y se estructura en siete pasos (figura 2).

Figura 2: Modelo Hong Kong

Fuente: adaptado de Arpí Miró et al. (2012) .

Planificación o Diseño de un ABP

El diseño de un ABP inicia con la formulación de los objetivos de aprendizaje y la creación del problema que se abordará con los estudiantes. Es fundamental comprender los criterios necesarios para plantear un buen problema en matemáticas. Preparar el problema antes de que los alumnos comiencen la aplicación es esencial en la fase de planificación o diseño del ABP. La creación del problema no es tarea sencilla, una formulación inadecuada puede llevar a que los grupos de trabajo enfrenten dificultades para aplicar sus conocimientos previos, lo que podría llevar a requerir más tiempo del previsto para resolverlo. Por lo tanto, es crucial prestar atención especial a la elaboración del problema (Jacobs et al., 2003; Zakaria et al., 2024).

En el enfoque del ABP, el problema exige que los estudiantes desarrollen habilidades de análisis, síntesis y evaluación, ya que estos problemas se relacionan con situaciones del mundo real, y no toda la información necesaria para resolverlos se encuentra directamente en el problema o en los materiales del curso (Chacón et al., 2020). Como resultado, los estudiantes deben realizar investigaciones, buscar nuevos recursos y tomar decisiones basadas en la información que adquieren. Además, es importante destacar que un mismo problema puede tener múltiples respuestas aceptables (Duch, 1996).

A continuación, se describen los pasos para el diseño del problema en un ABP de acuerdo con Romero Medina y García Sevilla (2008) :

1. Definir los objetivos curriculares específicos que se desean alcanzar con el problema. Estos objetivos representan los resultados de aprendizaje esperados y pueden centrarse en áreas donde las metodologías tradicionales sean menos efectivas. A veces, el problema puede surgir de manera espontánea a partir de noticias o casos relacionados con las necesidades curriculares.

2. Identificar un escenario relacionado con los objetivos curriculares es esencial. Por ejemplo, una noticia sobre el descubrimiento de una nueva fórmula matemática en la resolución de problemas de optimización puede servir como base para un problema que desafíe a los estudiantes a aplicar esta fórmula en situaciones prácticas de optimización.

3. Determinar la extensión del ámbito interdisciplinar del problema. Es importante definir cuán interdisciplinario será el problema. En el ejemplo mencionado, si existen disciplinas como economía o administración relacionadas, se puede incluir aspectos de esos campos en la descripción del problema.

4. Elaborar un primer borrador del problema, se recomienda colaborar con otros profesores que estén familiarizados con la metodología ABP para realizar una lluvia de ideas y mejorar el problema de manera conjunta.

5. Determinar la disponibilidad de recursos que los estudiantes necesitarán para abordar el problema, como las fuentes bibliográficas o recursos en línea.

6. Verificar minuciosamente el problema que se ha desarrollado al final del proceso. Para esto es esencial verificar el problema elaborado utilizando un conjunto completo de criterios para asegurarse de que incluye todos los elementos esenciales de un problema ABP.

7. Redactar documentos complementarios, esto incluye una breve introducción, los objetivos de aprendizaje relacionados con la disciplina, el problema y una lista de referencias que abarque fuentes de investigación y recursos recopilados.

8. Evaluar la calidad del problema elaborado. El problema debe cumplir criterios como: ser interesante para los estudiantes por razones sociales, cotidianas, académicas o profesionales. Además, debe reflejar la actualidad, tener objetivos multidisciplinarios, cubrir objetivos didácticos, adaptarse al nivel de los estudiantes, estar bien estructurado y ser lo suficientemente complejo como para requerir trabajo en equipo.

Evaluación en el ABP

La evaluación en el enfoque de ABP se basa en los resultados obtenidos al finalizar su implementación con los estudiantes. Para llevar a cabo esta evaluación, se utilizan rúbricas como una herramienta apropiada que permite establecer criterios de evaluación claros tanto para el proceso como para el aprendizaje. A continuación, se describen algunas de las rúbricas que pueden emplearse en un ABP (División Académica, 2019; Fundación Telefónica, 2014):

• Rúbrica del ABP: se utiliza para obtener la opinión de los alumnos sobre la experiencia del ABP realizado.

• Rúbrica de participación: se emplea para evaluar la participación individual de cada estudiante en las actividades cooperativas del ABP.

• Rúbrica del profesor: sirve para evaluar el desempeño del profesor durante la implementación del ABP.

Es importante aclarar que la evaluación tiene un carácter formativo, pues se concentra en el desarrollo integral del estudiante, promoviendo el pensamiento crítico, la autodeterminación y la confianza. En el ABP se fomenta la metacognición, permitiendo a los estudiantes planificar, monitorear y evaluar su propio aprendizaje, y se enfatiza el desarrollo de competencias transversales como la colaboración y la comunicación (Fook y Sidhu, 2019).

Para esto, es esencial crear entornos de aprendizaje colaborativos que promuevan el diálogo y la construcción conjunta del conocimiento. Las rúbricas del ABP evalúan la claridad y relevancia del problema, la calidad del proyecto final y la reflexión crítica de los estudiantes, mientras que las rúbricas de participación y del profesor miden la contribución individual, la colaboración, la responsabilidad y el desempeño del profesor en facilitar el aprendizaje. Estas reflexiones sobre la participación en la evaluación, la adaptabilidad y la flexibilidad, y el enfoque en el desarrollo integral de los estudiantes, no solo fortalecen la evaluación en el ABP, sino que también enriquecen el aprendizaje y el desarrollo de competencias y habilidades para la vida (Wei et al., 2021; Black y Wiliam, 2018; Fook y Sidhu, 2019).

ABP en Estadística I para Administración Pública Territorial

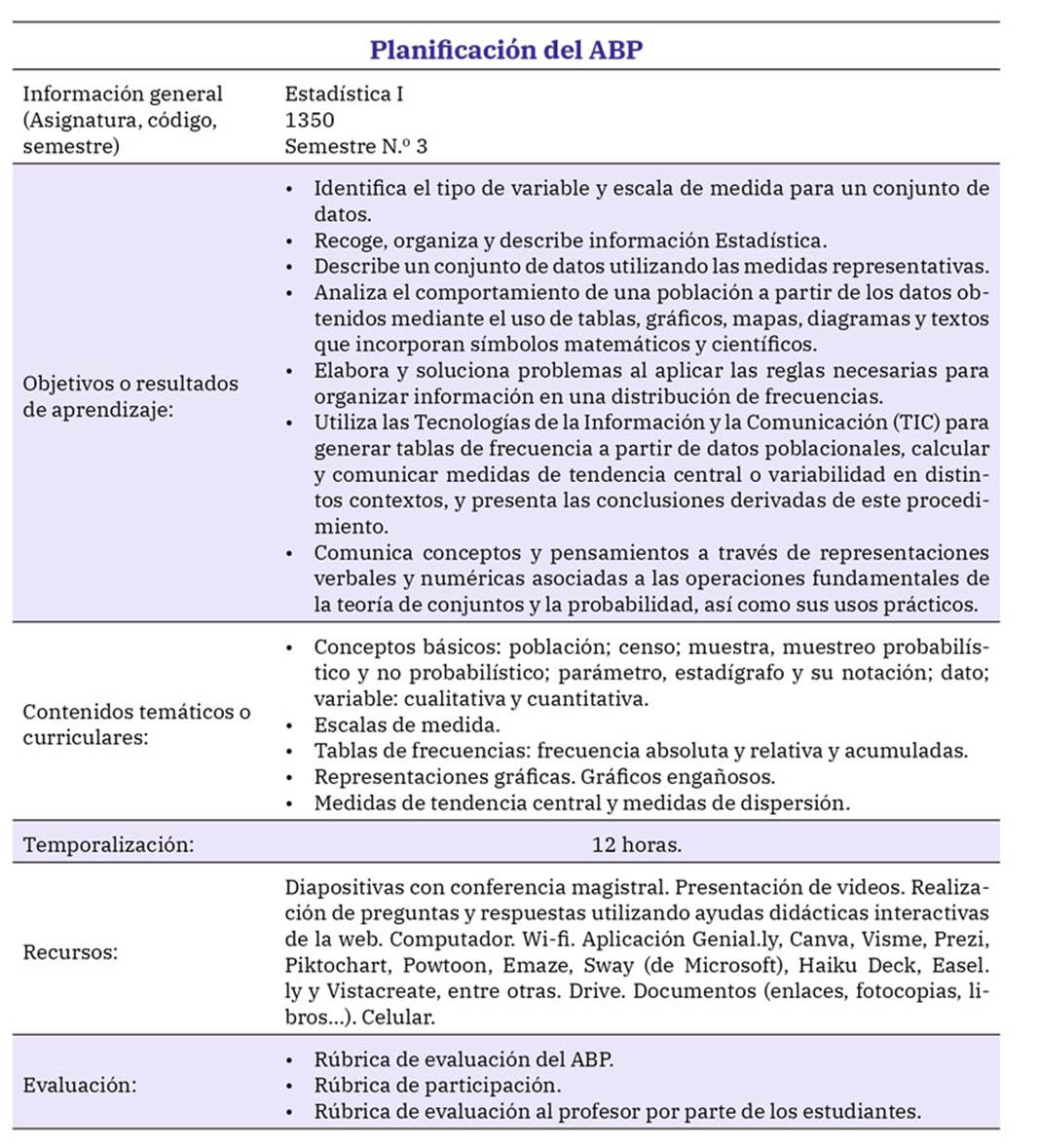
En este apartado se presenta un ejemplo del diseño de un ABP aplicado a la asignatura de Estadística I para el programa de APT de la ESAP. Se recomienda que este ABP sea aplicado en pequeños grupos colaborativos de 3 a 4 estudiantes. En la tabla 1, se pueden observar los pasos descritos anteriormente en el diseño o planificación de un problema y la evaluación.

Tabla 1: ABP en Estadística I para APT

Fuente: elaboración propia con base en el Microcurrículo de la Asignatura Estadística I de APT (ESAP, 2022b).

Escenario de desarrollo del ABP

La Oficina de Tecnologías de la Información y las Comunicaciones (OTIC) de la ESAP, dentro del servicio de software ofimático, tiene a disposición de los servidores de la Entidad las siguientes aplicaciones:

• Adobe Acrobat Reader, Adobe Photoshop.

• Autocad, 7-zip.

• Google Chrome, Internet Explorer, Mozilla Firefox, Safari, Flash Player.

• Word, Excel, PowerPoint, Outlook, Access, OneNote, Project, Publisher, SharePoint, Visio y Teams.

En este sentido, para conocer las aplicaciones de ofimática más utilizadas por el funcionariado, contratistas y comunidad universitaria en la operación de la ESAP, se llevará a cabo una encuesta con el propósito de responder las siguientes preguntas:

1. ¿Cuáles son los 10 tipos de aplicaciones ofimáticas más utilizadas según grupos etarios?

Para esto, se debe construir una tabla de frecuencias, considerando el ancho del intervalo sugerido (por edades): (10 - 20), (21 - 30), (31 - 40), (41 - 50), (51 - 60), (61 - 70).

1. Según la tabla de frecuencias, ¿cuáles son las 6 aplicaciones ofimáticas más utilizadas? Calcular el porcentaje de cada una.

2. Calcular, ¿cuál es la probabilidad de la aplicación ofimática más utilizada?

3. Basándose en la información obtenida, decidir qué tipo de aplicación la OTIC debería instalar en los equipos y justificar esta elección.

4. Calcular los estadígrafos de posición y dispersión que considere apropiados (no necesariamente todos), y justificar su elección.

5. Seleccionar cualquiera de las siguientes aplicaciones para presentar los resultados obtenidos mediante gráficas circulares o de barras, histogramas, pictogramas y tablas: Canva, Visme, Prezi, Piktochart, Powtoon, Emaze, Sway (de Microsoft), Haiku Deck, Easel.ly y Vistacreate. Luego, compartirlos con el resto de la clase.

Instrucciones y recomendaciones

De acuerdo con el escenario propuesto, se solicita a los estudiantes conformar grupos de 3 a 4 integrantes, a quienes se les darán las siguientes instrucciones:

1. La encuesta se realizará tomando como referencia el objetivo, la clasificación etaria y las aplicaciones ofimáticas. Cada equipo debe realizar 50 encuestas por un solo grupo etario, asignado por el docente.

2. Cada equipo deberá definir los roles que se asumirán en el grupo colaborativo para el desarrollo del ABP, así como designar al secretario del equipo para recopilar la información.

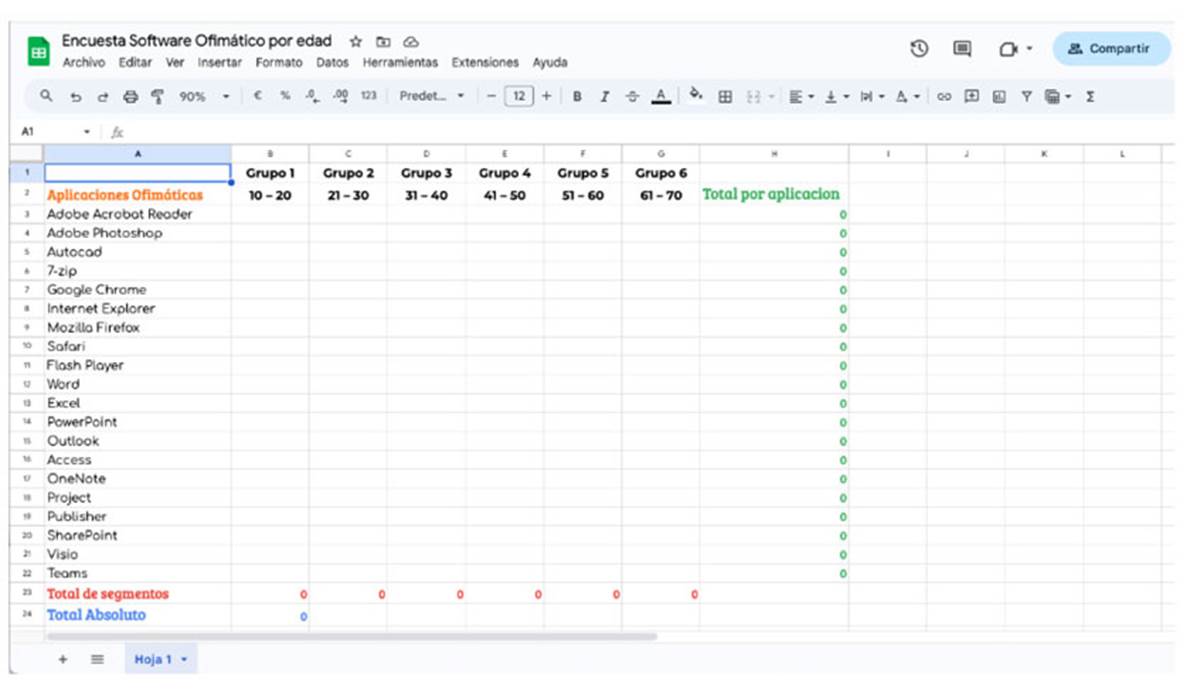
3. El secretario del equipo deberá digitar la información recopilada a través de un DRIVE, que contiene una hoja de cálculo elaborada previamente por el docente (figura 3). De esta manera, se obtendrá un resumen de la información recogida por todos los grupos colaborativos.

Figura 3: Hoja de cálculo sobre encuesta de Software Ofimático por edad.

Pasos para el desarrollo de un ABP de los estudiantes

El desarrollo de un ABP no se limita a proporcionar documentación y un problema. Inicialmente, no se espera que el estudiante sea completamente autónomo e investigue todas las posibles soluciones para posteriormente argumentar cuál es la mejor. Por lo tanto, el ABP se implementa con los estudiantes a través de pasos específicos que fomentan el trabajo autónomo y colaborativo, siempre con la orientación del docente (Vera Velázquez et al., 2021).

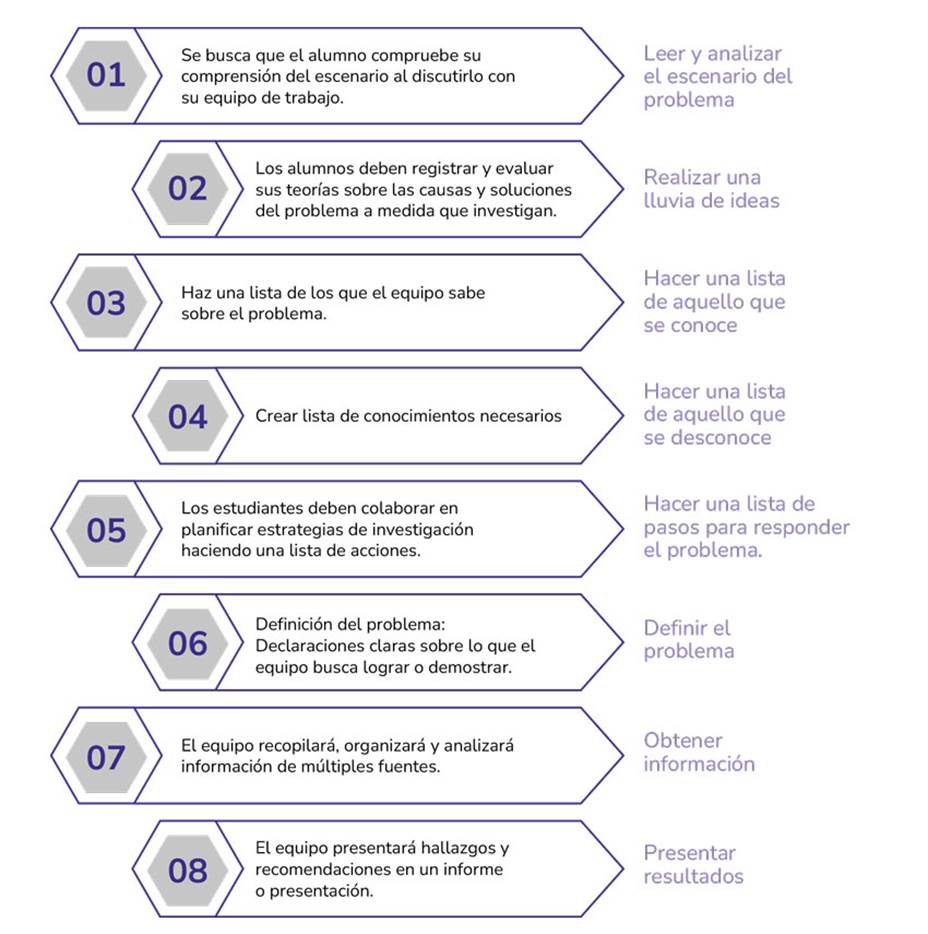
En la figura 4, se pueden observar los pasos descritos por Morales y Landa (2004) sobre el proceso de desarrollo del ABP, que sirven para orientar a los estudiantes en su aplicación.

Figura 4: Desarrollo del ABP según Morales y Landa (2004) .

El ABP es una metodología pedagógica que se adapta perfectamente a las necesidades de formación en APT, especialmente en áreas que requieren habilidades matemáticas y estadísticas. En el caso específico de la ESAP, la implementación del ABP en la asignatura de Estadística I ofrece una oportunidad única para abordar la actitud negativa hacia las matemáticas mientras se desarrollan competencias esenciales para futuros administradores públicos. El escenario propuesto, centrado en el análisis del uso de aplicaciones ofimáticas en la ESAP, ilustra cómo el ABP puede aplicarse de manera efectiva. Este problema real no solo contextualiza el aprendizaje de conceptos estadísticos, sino que también demuestra su relevancia directa en la gestión pública, siguiendo los pasos estructurados del ABP para guiar a los estudiantes desde la comprensión inicial del problema hasta la presentación de soluciones basadas en evidencia. La aplicación del escenario propuesto y los pasos que deben desarrollar los estudiantes se pueden interpretar de la siguiente manera:

1. Leer y analizar el escenario del problema: los estudiantes deberán comprender el contexto de la OTIC de la ESAP y las aplicaciones ofimáticas disponibles.

2. Realizar una lluvia de ideas: los grupos discutirán sobre las posibles causas y soluciones relacionadas con el uso de aplicaciones ofimáticas en diferentes grupos etarios.

3. Hacer una lista de aquello que se conoce: los estudiantes listarán las aplicaciones ofimáticas mencionadas y su conocimiento previo sobre estadística y encuestas.

4. Hacer una lista de lo que se desconoce: identificarán la información que necesitan obtener mediante la encuesta.

5. Hacer una lista de pasos para resolver el problema: planificarán cómo realizar las 50 encuestas asignadas y cómo analizarán los datos.

6. Definir el problema: clarificarán el objetivo de determinar las aplicaciones más utilizadas y tomar decisiones basadas en datos.

7. Obtener información: realizarán las encuestas y recopilarán los datos en la hoja de cálculo compartida.

8. Presentar resultados: analizarán los datos, calcularán estadísticas, crearán gráficos y presentarán sus hallazgos y recomendaciones.

Este escenario evidencia claramente la aplicación práctica del ABP, involucrando a los estudiantes en un problema real, fomentando el trabajo en equipo, la investigación y el análisis de datos, así como la toma de decisiones basada en evidencia.

Inicialmente, los estudiantes formulan hipótesis basadas en sus conocimientos previos y observaciones preliminares sobre los patrones de uso de aplicaciones entre diferentes grupos de edad. Por ejemplo, podrían suponer una mayor utilización de herramientas colaborativas en línea entre los usuarios más jóvenes (Ertmer et al., 2009). Posteriormente, deducen posibles resultados observables a partir de estas hipótesis, lo que les permite traducir conceptos abstractos en medidas concretas y verificables (Loyens et al., 2015).

La fase de recolección y análisis de datos, mediante la realización de encuestas y el examen de los resultados, ofrece a los estudiantes la oportunidad de contrastar sus hipótesis con evidencia empírica, subrayando la importancia de basar las decisiones en datos concretos (Naupas et al., 2023). Al comparar los hallazgos con sus predicciones iniciales, los estudiantes evalúan la validez de sus hipótesis originales. Este proceso es fundamental para fomentar el pensamiento crítico y la capacidad de revisar las propias ideas en función de la evidencia (Leary & Walker, 2023).

En síntesis, si los datos no respaldan las hipótesis iniciales, los estudiantes deben reformular sus planteamientos, lo que promueve la flexibilidad cognitiva y la comprensión del carácter iterativo del método científico (Muzaini et al., 2023).

Discusión

La implementación del ABP en la asignatura de Estadística I del programa de APT de la ESAP se presenta como una estrategia prometedora para abordar la actitud negativa hacia las matemáticas y mejorar el desempeño académico de los estudiantes. Los resultados esperados de esta propuesta se discuten a continuación, considerando hallazgos recientes en la literatura especializada sobre ABP.

En primer lugar, se anticipa una mejora significativa en la actitud de los estudiantes hacia las matemáticas. Estudios recientes como los de Vélez Córdova et al. (2022) , Lavado-Puente et al. (2023) y Pacheco-García y Cáceres-Mesa (2024) , han demostrado que el ABP puede transformar positivamente las percepciones de los estudiantes sobre las matemáticas al contextualizar su aprendizaje en situaciones reales. Según Dolmans (2019) , el ABP fomenta una mayor motivación intrínseca y un compromiso más profundo con el material de estudio, lo que podría ayudar a superar la ansiedad matemática comúnmente observada en estudiantes de ciencias sociales.

Se espera que la aplicación del ABP en el contexto de la APT mejore la comprensión de los conceptos estadísticos y su relevancia práctica. Moallem et al. (2019) encontraron que el ABP mejora significativamente la retención de conceptos y la capacidad de aplicarlos en situaciones reales, especialmente en campos que requieren habilidades de resolución de problemas complejos, como la administración pública.

Además, se prevé un aumento en la motivación y el compromiso de los estudiantes con el aprendizaje de las matemáticas. Chen et al. (2021) demostraron que el ABP no solo mejora el rendimiento académico, sino que también aumenta la autoeficacia de los estudiantes en matemáticas, un factor crucial para superar las actitudes negativas preexistentes.

Sin embargo, es importante reconocer los desafíos potenciales en la implementación del ABP. Wijnia et al. (2015) señalan que la transición a metodologías activas como el ABP puede encontrar resistencia inicial por parte de estudiantes y docentes acostumbrados a métodos más tradicionales. Será crucial proporcionar apoyo adecuado y formación a los instructores para garantizar una implementación efectiva.

Adicionalmente, se espera que esta propuesta contribuya a cerrar la brecha entre la teoría y la práctica en la formación de administradores públicos. Hallinger & Bridges (2021) argumentan que el ABP es particularmente efectivo en la educación de gestión y liderazgo, ya que prepara a los estudiantes para los desafíos del mundo real que enfrentarán en su carrera profesional.

En conclusión, la implementación del ABP en la asignatura de Estadística I del programa APT de la ESAP se presenta como una estrategia viable y prometedora para mejorar la actitud hacia las matemáticas y potenciar las habilidades cuantitativas de los futuros administradores públicos. Los resultados esperados están respaldados por la literatura reciente sobre ABP, aunque se reconoce la necesidad de una cuidadosa planificación y seguimiento para maximizar su efectividad.

Conclusiones

La actitud de los estudiantes hacia las matemáticas es un factor crucial que impacta su capacidad para aprender y aplicar conceptos matemáticos, y la negatividad hacia esta materia puede afectar significativamente el éxito académico y profesional, especialmente en campos como la administración pública. Abordar este desafío en la formación de administradores públicos es esencial, dado que las habilidades matemáticas son fundamentales para la gestión efectiva.

El Aprendizaje Basado en Problemas (ABP) se presenta como una estrategia pedagógica altamente efectiva para superar el estigma asociado a las matemáticas. Al contextualizar el aprendizaje mediante la resolución de problemas reales, el ABP facilita la aplicación práctica de conceptos matemáticos y fomenta el desarrollo de habilidades de resolución de problemas, lo cual es crucial para la formación en APT. Esta metodología no solo mejora la relevancia de las matemáticas en la carrera futura de los estudiantes, sino que también requiere una capacitación adecuada de los docentes para su implementación exitosa.

La evaluación dentro del ABP debe ser formativa y comprensiva, utilizando rúbricas que contemplen tanto el proceso como el resultado final del aprendizaje. Esto incluye la retroalimentación de los alumnos, la participación individual y el desempeño del profesor, promoviendo habilidades esenciales como la colaboración y la comunicación.

Un ejemplo concreto de la implementación del ABP en la asignatura de Estadística I para APT ilustra cómo este enfoque puede transformar la enseñanza de las matemáticas, facilitando la toma de decisiones y ofreciendo una experiencia de aprendizaje significativa y relevante.