Marco teórico

La teoría económica del efecto Fisher examina la relación entre las tasas de interés nominales y la inflación esperada. Fisher (1930) plantea la hipótesis de que la tasa de interés nominal se ajusta conforme a los cambios en la tasa de inflación esperada, de modo que la tasa de interés real permanece constante. Este efecto puede ser sustentado debido a que, en el largo plazo, los agentes económicos no experimentan ilusión monetaria¹ en la economía, lo que permite que el fenómeno se cumpla. El tipo de interés real está determinado por la interacción que se presenta entre la demanda y la oferta de los recursos financieros disponibles, que reflejan la dinámica del sector real de la economía. Por otro lado, la tasa de interés nominal es la suma de la tasa de interés real y la tasa de inflación prevista. Esta relación puede expresarse a través de la siguiente ecuación:

Donde R _t representa la tasa de interés nominal, r _t es la tasa de interés real ex ante y expresa la inflación esperada. Esta ecuación captura la relación implícita entre la inflación esperada y la tasa de interés nominal, con lo que un cambio en se traduce de manera completa en un cambio en R _t , debido a que se asume la estacionariedad del tipo de interés real ex ante, como sugieren diversos autores, entre ellos MacDonald y Murphy (1989), Ferrer (1998) y López y Reyes (2007). En el largo plazo, esta tasa alcanzará su nivel de equilibrio, lo que permite establecer la relación del efecto Fisher de la siguiente forma:

Aquí, β₀ representa el valor promedio constante a largo plazo del tipo de interés real esperado, y puede considerarse como una estimación de la tasa de interés real de equilibrio, siempre que β₁ =1. Por su parte β₁ es el parámetro de inflación, de modo que representa la forma como responde el tipo de interés nominal frente a cambios en la inflación esperada. No obstante, considerando el supuesto de expectativas racionales (Badillo Amador et al., 2010; Bajo-Rubio y Esteve, 1998), se plantea un contexto de información total, asumiendo que los agentes tienen conocimiento completo de la información disponible para pronosticar sus expectativas de inflación; por lo tanto, la inflación esperada se explica como la inflación observada π_t, más un término de error aleatorio ε, de tal forma que cumple la siguiente forma funcional:

De esta manera, la inflación efectiva es una buena aproximación de la inflación esperada, con lo que podemos sustituir la ecuación (3) en la ecuación (2), para llegar a la siguiente expresión:

En este contexto, γ captura los choques que impactan el componente estacional de la tasa de interés real, así como la suma del término de error del pronóstico basado en el supuesto de racionalidad de la inflación. Para validar el efecto Fisher, es necesario que tanto la inflación como la tasa de interés nominal tengan una raíz unitaria, lo que permitiría establecer una relación de largo plazo. Además, está validación se determina por β₁, en el sentido de que, si este coeficiente es igual a 1, se puede concluir que cualquier variación en la tasa de inflación se refleja completamente en la tasa de interés nominal, manteniendo constante la tasa de interés real. Esto implica que, a largo plazo, los aumentos en la inflación se trasladan de manera proporcional a la tasa de interés nominal, permitiendo llegar al cumplimento del efecto Fisher completo. Se acepta que la tasa de interés es un mal indicador para la política monetaria, pero logra predecir de manera efectiva la inflación; por otro lado, se acepta la neutralidad del dinero.

Por su parte β₁ si es menor que 1, se produce un efecto Fisher parcial, donde cualquier variación en la tasa de inflación esperada se reflejará menos que proporcionalmente al tipo de interés nominal, debido a una ilusión monetaria parcial. Una posible explicación es que una mayor inflación impulsa a los agentes económicos a reemplazar dinero por capital, lo que incrementa los precios de los activos y disminuye los tipos de interés reales.

Literatura empírica

El efecto Fisher, que postula una relación de largo plazo entre las tasas de interés nominales y la inflación esperada, ha sido ampliamente estudiado en diferentes contextos económicos. Sin embargo, su validez empírica sigue siendo objeto de debate, particularmente en economías emergentes como la colombiana. En este contexto, es esencial evaluar las diferencias regionales y los factores específicos que pueden influir en esta relación. Este análisis busca no solo sintetizar los principales hallazgos en la literatura sobre el efecto Fisher, sino también resaltar las limitaciones metodológicas y las posibles líneas de investigación futura para un análisis más detallado a nivel regional.

Se parte de diversas aproximaciones del efecto Fisher, que nos ayudarán a contrastar y direccionar la investigación, debido a que los resultados obtenidos por las diferentes investigaciones permiten contextualizar y afianzar los conocimientos del tema. En el trabajo de Cárdenas y Sáenz (2001), se examina el efecto en Colombia durante el periodo 1980-2000, utilizando datos trimestrales sobre la tasa de interés nominal y la tasa de inflación. La metodología empleada incluye técnicas econométricas como pruebas de raíces unitarias y cointegración, así como, específicamente, las pruebas de Dickey-Fuller, KPSS y Johansen, para evaluar la estabilidad y la relación de largo plazo entre las variables. Los resultados demostraron que tanto la tasa de interés nominal como la inflación tienen una raíz unitaria y están cointegradas, lo que sugiere una relación de largo plazo, por lo cual se concluye del análisis que el coeficiente de inflación es igual a uno, con lo que se consigue el efecto Fisher completo.

A pesar de que se confirma este hecho, es crucial considerar que existen limitaciones en el estudio, como lo pueden ser la sensibilidad del tamaño de la muestra y las variables utilizadas. De aquí se deriva que diferentes condiciones podrían mostrar un efecto Fisher parcial o inexistente, lo cual sugiere la necesidad de incluir otras variables o considerar cambios estructurales en el análisis. Este trabajo contribuye a la validación empírica del efecto Fisher y destaca la importancia de las expectativas inflacionarias en la política monetaria y financiera, si bien se resaltan las limitaciones que pueden llegar a tenerse en el desarrollo de la investigación y que podrían afectar a los resultados del trabajo. En ese sentido, cabe resaltar por ejemplo cómo Rodríguez et al. (2021), en su proceso de evaluación del efecto Fisher en Colombia durante el periodo 1991-2020, por medio de una metodología corrección de errores, llegaron a la conclusión de que para el periodo de estudio existió un efecto Fisher parcial en el país, lo cual contrarresta con los resultados obtenidos por Cárdenas y Sáenz (2001).

Como resultado, lo anterior indica que la teoría de la neutralidad del dinero no se cumple. En el caso de la economía colombiana, una inflación baja y estable actúa como un impuesto sobre el dinero, impulsando a los agentes a invertir en otros activos y ejerciendo presión a la baja sobre las tasas de interés reales, lo cual lleva a un incumplimiento parcial del efecto Fisher.

Por otra parte, el artículo de Briceño y Jiménez (2008) buscó validar la hipótesis de Fisher en el contexto mexicano con datos mensuales desde 1985 a 2006, a fin de evaluar la estabilidad de las relaciones entre la inflación esperada y la tasa de interés nominal en un horizonte temporal de largos periodos. Los resultados reflejaron que existe una relación de largo plazo significativa y estable entre las tasas nominales de interés y la inflación esperada; en consecuencia, están cointegradas y los ajustes a corto plazo muestran que las variaciones en las tasas de interés nominal responden menos que proporcionalmente a los cambios en la inflación esperada, lo cual es consistente con el efecto Mundell-Tobin, dando como resultado un efecto Fisher parcial.

Según se evidencia en la revisión de literatura hecha por Badillo Amador et al. (2010), los resultados de numerosos estudios previos han reflejado inconsistencias en los resultados, lo que ha generado dudas sobre la validez del efecto Fisher en la práctica. Westerlund (2008) identificó dos desafíos principales a los que se enfrentan las diferentes investigaciones: la baja potencia de los test de cointegración y el tamaño muestral, que en algunos estudios es limitado. Estos problemas llevaron a la sugerencia del uso de datos de panel, que combinan información temporal y transversal, lo que podría proporcionar una perspectiva más robusta. En este contexto, Badillo Amador et al. (2010) proponen investigar la existencia y naturaleza del efecto Fisher en la UE utilizando datos de panel trimestrales de quince países desde 1983 hasta 2009.

Los resultados de las pruebas de cointegración en series temporales revelaron falta de evidencia consistente en torno a una relación de equilibrio a largo plazo entre la tasa de inflación y el tipo de interés nominal para la mayoría de los países individuales. Sin embargo, al aplicar técnicas de cointegración a datos de panel, se identificó una relación estable a largo plazo entre ambas variables en el conjunto de países de la UE, sugiriendo que factores comunes, como los choques del petróleo y las conexiones financieras entre países, pueden tener un impacto significativo en la relación entre inflación y tasas de interés. Los hallazgos fueron confirmados por la estimación del parámetro de cointegración mediante el método DOLS (Dynamic Ordinary Least Squares), que mostró un coeficiente cercano a 1, validando el efecto Fisher en su versión más rigurosa. Estos son resultados que tienen importantes implicaciones para la política monetaria, en particular para el Banco Central Europeo.

También, resulta importante indagar sobre la repercusión que tuvo la pandemia en este efecto. Al respecto, Colmán et al. (2022) centran su análisis en la inflación en Paraguay a raíz de la pandemia de COVID-19, utilizando un enfoque sobre los efectos de los shocks monetarios transitorios y permanentes de la inflación, las tasas de interés y la actividad económica. La metodología implementada por los autores fue un modelo semiestructural de crecimiento del producto, inflación y tasas de interés, con dos modelos estimados para los periodos 1994-2022 y 2004-2022. De los resultados se encuentra que el componente permanente de la inflación explica el 4,74 % de los cambios en la inflación para el periodo 2004-2022 y el 66,25 % para 1994-2022. Un hallazgo crucial es la evidencia a favor del efecto neo-Fisher, que indica que un shock permanente en la tasa de interés nominal influye en la inflación tanto a corto como a largo plazo, sin causar una contracción en la actividad económica agregada. Esto es coherente con la teoría del efecto Fisher, que establece una relación positiva entre la tasa de interés nominal y la inflación a largo plazo, subrayando además la importancia de las expectativas inflacionarias en la determinación de los resultados económicos inmediatos y futuros en Paraguay. La investigación sugiere que las políticas monetarias deben tener en cuenta estos efectos y comunicarse de manera clara para anclar las expectativas inflacionarias. En conclusión, aunque la literatura existente proporciona un panorama amplio sobre el efecto Fisher, es fundamental considerar las particularidades regionales y los factores externos que pueden influir en esta relación.

Descripción de los datos

En esta investigación se analiza el impacto del efecto Fisher, considerando como variables clave la tasa de inflación y los certificados de depósito a término (CDT) a noventa días, a partir de datos proporcionados por el Banco de la República de Colombia (BanRep). El objetivo es examinar si en el país, durante el periodo de estudio, la relación postulada por el efecto Fisher se mantiene y precisar cómo la inflación ha influido en las tasas de interés nominales.

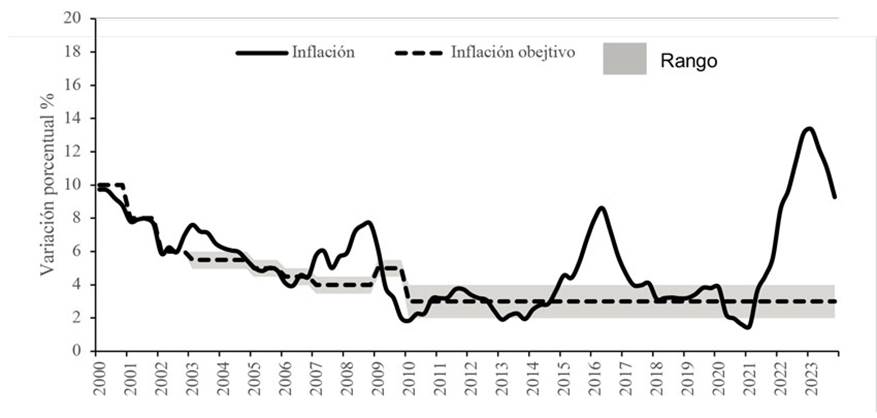
Destacando las dinámicas entre la inflación y la tasa de interés CDT a noventa días, en la figura 1 podemos ver que, dada la relación inherente del Banco Central y la inflación, se destacan dos momentos en el tiempo: el primero se relaciona con la meta de inflación establecida antes del 2000 de 10 p.p., la cual conservó una tendencia a la baja, junto con el hecho de establecer un rango alrededor de la meta a comienzos del 2003 (+/− 0,5 p.p.), en una dinámica que abarcó de 2000 a 2009; por otra parte, el segundo lapso de tiempo está vinculado con el objetivo actual de 3 p.p., junto con un rango más amplio ( +/− 1 p.p. ), a lo largo del periodo 2010-2023.

Figura 1: Comportamiento de la inflación reportada (2000-2024)

Fuente: elaboración propia, datos tomados de BanRep

Durante el primer momento, la inflación se enfrentaba en un contexto de recuperación económica, derivado de la crisis financiera de 1999, con niveles de crecimiento del PIB de -4,5 %, altos niveles de desempleo y una inflación de dos dígitos, aspectos todos que dificultaban la estabilidad macroeconómica. En ese contexto, los primeros niveles de inflación reportados a partir del 2000 estuvieron en parte explicados por la crisis asiática de 1997 y la fuerte depreciación del peso. Frente a dicho escenario, el Banco Central, en su esfuerzo por cumplir con su mandato constitucional, optó por fijar en 2003 una nueva meta de inflación adyacente con un rango de 0,5 p.p. alrededor de la meta. Debido al compromiso con la estabilidad de precios, la métrica fue reduciéndose de manera gradual, estableciendo metas más bajas, para poder influir de manera efectiva en las expectativas de inflación. Todas estas medidas, acompañadas del buen desempeño económico de Colombia, contrastaron con niveles favorables de crecimiento del PIB.

En este periodo, los choques más significativos tuvieron lugar a lo largo de 2007 y 2008, debido a dos factores principales: los altos precios del petróleo y la disminución de la demanda mundial como resultado de la crisis financiera de 2008, eventos ambos que aumentaron los costos de producción y transporte a nivel global. Para poder contrarrestar el primer factor, Colombia dispuso la creación de un fondo de estabilización de precios del petróleo (FEPC); sin embargo, respecto del segundo factor, la crisis financiera depreció el peso dado que las fluctuaciones en el tipo de cambio impactaron los precios de los bienes importados, contribuyendo a la inflación. Durante este primer lapso la inflación se mantuvo en promedio en 6 p.p. y el cambio más significativo fue la crisis financiera de 2008, afectada por el bajo nivel de demanda mundial, la depreciación y los precios del crudo.

En el periodo siguiente, que abarcó desde 2010 hasta 2023, se logró una estabilidad notable tanto en el nivel de precios como en el crecimiento económico, lo cual se atribuyó a la recuperación económica inicial de 2010 y a la implementación de una nueva meta de inflación del 3 %, junto con el buen manejo previo de la política monetaria. Con todo, se presentaron también impactos asociados a la caída en los precios internacionales de petróleo de 2014-2015 y la crisis sanitaria de 2019.

Para 2014 y 2015, el primer evento provocó una tasa de cambio depreciada, con menos ingresos en dólares. Esta depreciación alcanzó en 2015 niveles superiores a 3000 COP, con fluctuaciones en el valor del peso colombiano frente al dólar estadounidense que influyeron en los precios de los bienes importados, agravando la inflación. La tasa de cambio se mantuvo alrededor de los 3000 COP para los siguientes años, si bien la inflación empezó a presentar muestras de una desaceleración, regresando gradualmente a niveles más controlados.

Por su parte, la pandemia de COVID-19 limitó la subida de precios, aunque en el periodo postpandemia el incremento en la inflación no logró ser controlado, debido en parte a factores globales, como la guerra en Ucrania. Si bien se constató un alza en las expectativas inflacionarias para este momento, la inflación en promedio estuvo cercana a 4 p.p., un nivel más bajo que el del periodo 2000-2009, a pesar los choques significativos a la economía. A lo largo de ambos lapsos, el Banco Central cumplió sus metas de inflación en un 64 p.p. trimestralmente y en un 66 p.p. anualmente, un desempeño que favoreció tanto a la economía colombiana como al mismo banco, posicionándolo como una de las instituciones centrales más efectivas en el cumplimiento de sus objetivos constitucionales.

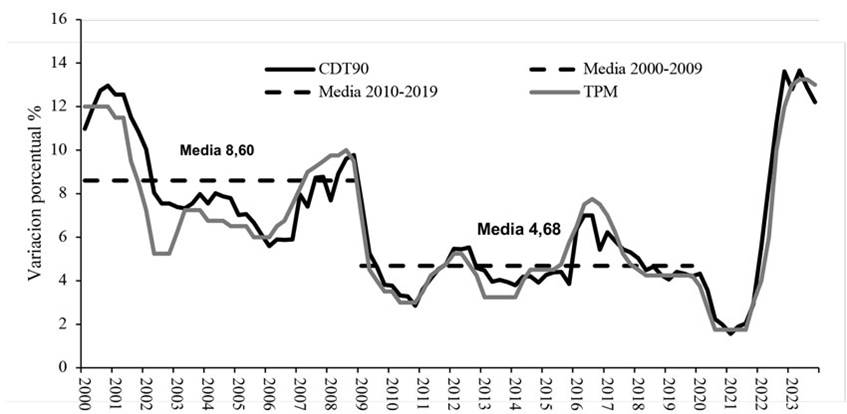
La figura 2 ilustra el modo en que la hipótesis de Fisher cobra relevancia, dada la dinámica de la tasa de interés de los CDT a noventa días, estrechamente ligada a la conducta de la tasa de interés de intervención por parte del banco, con un coeficiente de correlación fuerte de 0,95, además de un mecanismo de transmisión sobre las demás tasas más directo a los hogares, evidenciando un comportamiento de tasas sujeto a la dinámica de la inflación. Debido a ello, podemos considerar el análisis centrado en dos cambios estructurales. El primero de ellos se da en el año 2000, cuando la tasa de interés presentaba niveles restrictivos para mitigar los efectos de la crisis financiera de 1999, lo que logró que para 2001 y 2002 la inflación se fuera reduciendo en 1 p.p. cada año, algo que se vio reflejado en tasas interés más bajas, si bien en 2003 se presentó una sorpresiva inflación al alza. Pero el comportamiento trascendental se presentó entre 2007 y 2008, cuando la crisis financiera y los elevados precios del petróleo llevaron a la depreciación del peso, contribuyendo así a la inflación. En consecuencia, la autoridad monetaria elevó prudentemente las tasas para mitigar el choque a nivel mundial, observándose en este periodo una tasa de interés promedio de 8,60, lo que dio lugar a un primer cambio estructural, consistente con la recuperación económica de 2009, con tasas cercanas a 4 p.p., evidencia de la política monetaria expansiva tomada por parte del banco. En los años siguientes, el comportamiento no fue volátil, pese a que en 2016 se tomaron medidas debido al incremento en precios por el fenómeno de El Niño. De manera directa, el banco respondió con una política monetaria restrictiva para apaciguar esta leve subida. Las tasas de interés se fueron reduciendo paulatinamente hacia los niveles de inflación, hasta el choque sanitario de 2019, momento en que las tasas de interés bajaron a niveles cercanos a 1,75 para la TPM y 1,56 para los CDT, evidenciando la postura de una política monetaria expansiva por parte del Banco Central y de las demás entidades bancarias. Con todo, esta medida fue transitoria, pues al momento de la reactivación económica la guerra entre Rusia y Ucrania vino a elevar los precios y someter a una inminente postura restrictiva en las tasas.

Figura 2: Comportamiento de los CDT (2000-2024)

Fuente: elaboración propia, datos tomados de BanRep

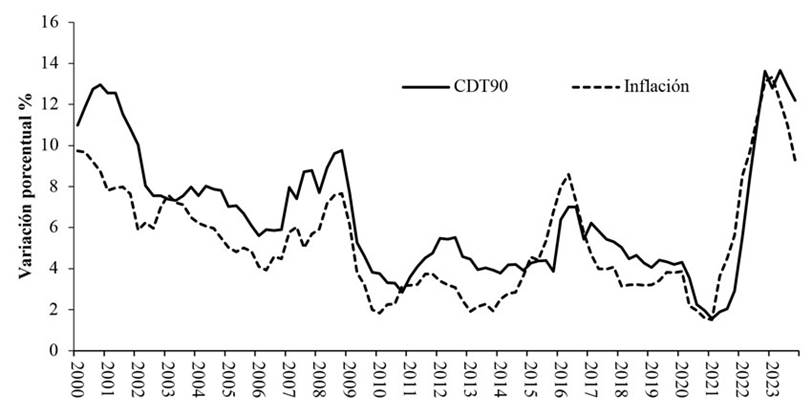
Establecido lo anterior, la figura 3 muestra la relación de las dos variables, que además presentan un comportamiento unísono, con un coeficiente de correlación de 0,85, indicador de una correlación fuerte tanto para inflación como para la tasa de interés nominal, expresada por la tasa de interés de los CDT a noventa días.

Figura 3: Variación porcentual de los CDT (tasa nominal) y la inflación (2000-2024)

Fuente: elaboración propia, datos tomados de BanRep

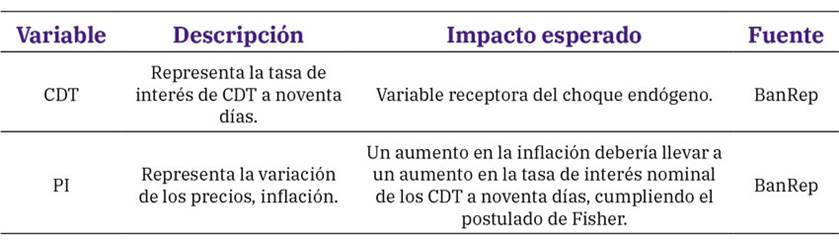
En la tabla 1 se describe de manera detallada el impacto de las variables. Se espera que la variable de la tasa de interés de CDT a noventa días absorba el choque de aumentos en la inflación, para evidenciar el efecto causal de esta variable, tal como afirman Rodríguez et al. (2021). Además, se observa un efecto Fisher parcial. En contraste, Cárdenas y Sáenz (2001) presentan un efecto Fisher completo para la economía colombiana. Estos son dos resultados que podrían esperarse en la investigación.

Tabla 1: Resumen e impacto esperado de las variables

Fuente: elaboración propia

Modelo econométrico

El análisis econométrico permitirá evaluar el modo en que los movimientos en la inflación se reflejan en las tasas de interés nominales, conforme postula el efecto Fisher. Para validar empíricamente esta hipótesis sobre la transmisión completa o parcial de los cambios en la inflación esperada a las tasas de interés nominal, se sigue el estudio propuesto por Cárdenas y Sáenz (2001), quienes analizaron la existencia de un efecto Fisher completo en la economía en Colombia, empleando técnicas de cointegración. Con base en esta investigación, se realiza una extensión utilizando un modelo multivariado de series de tiempo tipo VEC, con el objetivo de evaluar si el efecto Fisher continúa teniendo validez y si su efecto es completo, parcial o inexistente en la economía colombiana durante el periodo comprendido entre 2001 y 2023. Esta sección se divide en dos partes: la primera detalla la estimación del modelo, mientras que la segunda se enfoca en las pruebas realizadas para verificar la validez del modelo.

Estimación del modelo

Dentro de los modelos multivariantes de series temporales, destacan los modelos VEC, ampliamente utilizados para analizar series temporales integradas, es decir, aquellas que presentan una relación de largo plazo entre sí. Estos modelos permiten capturar tanto las relaciones de equilibrio a largo plazo como la dinámica de corto plazo entre las variables. En particular, consideran el efecto dinámico que puede generar un shock o una innovación no anticipada en una variable sobre las demás que conforman el sistema.

En razón a ello, se configura la estructura empírica del modelo utilizado en esta investigación, en la cual se considera la tasa de interés de CDT a noventa días como una variable proxy a la tasa de interés nominal, toda vez que tiene una relación directa con los hogares, bajo una perspectiva de inversión, y a la tasa de inflación efectiva. Se busca evaluar empíricamente si el efecto Fisher continúa teniendo valides y su efecto es completo, parcial o inexistente en la economía colombiana. El modelo VEC utilizado en este trabajo se expresa en la ecuación 5:

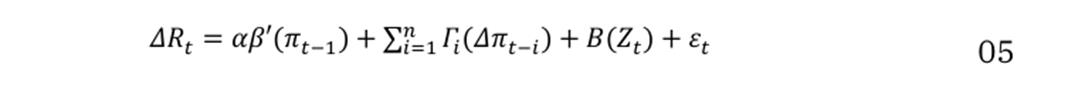
Donde el subíndice se refiere al número de rezagos óptimos para Colombia. En el lado izquierdo, ΔR_t se refiere a la tasa de interés nominal en diferencias en el tiempo t del modelo. En el lado derecho, hay un vector a α_i = (α_1,…, α_i ) que multiplica el vector de cointegración transpuesto β’ _i=( β’₁,… , β’_i ), y la tasa de inflación efectiva que representa el supuesto de expectativas racionales, lo cual convierte a la tasa de inflación esperada en la efectiva en niveles en el periodo t-1². Asimismo, Γ_i es una matriz que multiplica el vector B(z_t) de la tasa de inflación efectiva en primera diferencia y, por último, la matriz de coeficientes involucra variables dicotómicas que pueden modelar efectos estacionales para controlar los efectos de valores extremos atípicos³.

Sin embargo, hay que tener en cuenta que los coeficientes asociados a los modelos VEC pueden reportar una serie de grandes valores que exigen un análisis conjunto de los mismos a través de la cuantificación del impacto a corto y largo plazo de los shocks aleatorios sobre las variables endógenas explicativas, así como entender de qué manera afectan estas perturbaciones estocásticas a la evolución de las variables del sistema. Para este último aspecto, es necesario estimar la función de equilibrio a largo plazo y la ecuación de velocidad de ajuste.

Pruebas realizadas

A la hora de estimar modelos de series temporales multivariantes, es esencial verificar una serie de supuestos mediante pruebas estadísticas para garantizar su robustez (ver Apéndices). En primer lugar, debe determinarse el orden de integración de las variables, crucial para especificar si las variables deben estimarse en niveles con intercepto o tendencia, en primera o segunda diferencia. En esta investigación, dado que se estima un modelo VEC, las variables deben tener raíz unitaria en sus niveles; sin embargo, no deben tenerla en las primeras diferencias. En consecuencia, utilizamos la prueba de Phillips-Perron⁴ para confirmar que no son estacionarias en niveles, pero que sí lo sean cuando se considera la primera diferencia.

Tras verificar que las series presentan raíz unitaria en niveles y son estacionarias en primera diferencia, es necesario establecer el número adecuado de rezagos para el modelo VEC. Esto se logra mediante la prueba de Chi-cuadrado para determinar la exclusión de rezagos⁵, en la que se utilizan valores p inferiores al 5 %. Mientras que los p-valores sugieren utilizar entre cuatro y seis rezagos, siguiendo a Gujarati (2006), tras la estimación de un modelo de series de tiempo con datos trimestrales es aconsejable realizar la estimación con mínimo seis rezagos. A continuación, es necesario determinar el orden de cointegración de las variables del sistema, para lo cual se aplican las pruebas de traza y de valor propio máximo de Johansen⁶ a fin de identificar el número de relaciones de cointegración posibles en el modelo. En esta investigación, se confirmó la existencia de al menos una relación de cointegración a largo plazo, lo que permitió proceder con la estimación del modelo VEC⁷.

Posteriormente, se verifica la estabilidad dinámica del modelo, asegurando que las variables vuelven a sus niveles de equilibrio dinámico a largo plazo, tras identificar variaciones en el vector de innovaciones. En nuestra investigación, estimamos las raíces inversas del polinomio autorregresivo⁸ para confirmar la estabilidad del modelo VEC, concluyendo que la estimación es estable. A continuación, se revisan dos supuestos adicionales del modelo VEC: en primer lugar, evaluamos si la varianza de los residuos es constante utilizando la prueba de heteroscedasticidad de White sin términos cruzados⁹, concluyendo que los residuos son homocedásticos; en segundo lugar, se verifica la ausencia de correlación serial mediante la prueba del multiplicador de Lagrange¹⁰, confirmando que no existe autocorrelación entre los rezagos aplicados en el modelo.

Por último, se realizó la prueba de normalidad¹¹ de los residuos del modelo, que evalúa la distribución asintótica de los residuos en el modelo VEC estimado. Este paso se basa en la premisa de cumplir con los supuestos de errores no correlacionados y homocedasticidad, como sugiere Johansen (1995), quien señala la importancia de verificar que los residuos no se desvíen significativamente del supuesto de ruido blanco. Para cumplir este supuesto, en esta investigación se realiza una revisión detallada de los valores atípicos en los residuos del modelo VEC para crear las variables dicotómicas de normalidad exógena que se incluyen en el modelo. Asimismo, se realiza la prueba para confirmar el cumplimiento de este supuesto y validar la normalidad de los residuos.

Análisis de los resultados

Una vez realizadas las pruebas estadísticas correspondientes para verificar la consistencia del modelo propuesto, se procede a validar empíricamente la hipótesis del efecto Fisher sobre la transmisión completa o parcial de los cambios en la inflación esperada a las tasas de interés nominal. En este sentido, se presenta una argumentación basada en la evidencia empírica resultante de las ecuaciones a corto y largo plazo sugeridas por el modelo VEC.

Primero, tras establecer que cada una de las variables en esta investigación cumple con un orden de integración y confirmar la existencia de una relación de cointegración, se identifica un vector de cointegración, lo que sugiere un equilibrio a largo plazo (1, -0,95). Esto permite utilizar la función de equilibrio de largo plazo para evaluar si el efecto Fisher sigue siendo válido y determinar si se puede considerar completo, parcial o inexistente en la economía colombiana durante el periodo de 2001 a 2023.

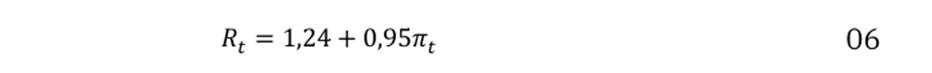
Ahora bien, el modelo macroeconométrico estimado en esta investigación mantiene la misma especificación que la prueba de cointegración de Johansen. El modelo VEC correspondiente es el siguiente:

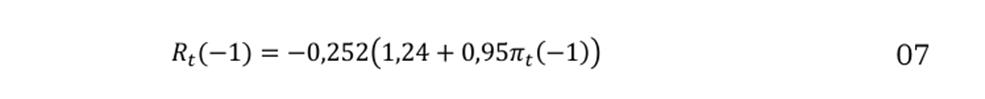
Donde 0,252 representa la velocidad de ajuste, que es estadísticamente significativa. Un valor más cercano a cero indica que el equilibrio a largo plazo se alcanza más rápidamente. A su vez, como se mencionó anteriormente, los residuales del modelo VEC estimado, como resultado, tienen un orden de integración cero en el largo plazo , indicador de que la relación de cointegración no tiene raíz unitaria, lo que implica que las series están cointegradas a largo plazo. Por lo tanto, la ecuación (5) se considera una especificación adecuada para evaluar si el efecto Fisher sigue siendo válido, y determinar si su impacto es completo, parcial o inexistente en la economía colombiana.

En este contexto, si la tasa de inflación efectiva aumenta en un 1 %, la tasa de interés nominal se incrementaría en un 0,95 %, evidenciando una relación directa entre la inflación observada y la tasa de interés nominal en la economía colombiana. Sin embargo, se concluye que, aunque el efecto Fisher está presente durante el periodo estudiado, es inferior a 1, lo que sugiere que es parcial. Esto significa que las variaciones en la tasa de inflación esperada se trasladan al tipo de interés nominal en menor medida de lo esperado, debido a una ilusión monetaria parcial. Con esto, se puede inferir que la relación parcial entre la tasa de inflación y la tasa de interés nominal en Colombia refleja una respuesta incompleta a los cambios en la inflación por parte de los agentes económicos y las políticas monetarias. Este desajuste tiene implicaciones significativas a nivel macroeconómico, como el aumento de la incertidumbre económica y la alteración de las decisiones de inversión y consumo, y al mismo tiempo repercute en la inestabilidad financiera, ya que los agentes económicos podrían no ajustar sus expectativas inflacionarias de forma proporcional a los cambios en las tasas nominales.

Una posible explicación es que una mayor inflación induce a los agentes económicos a reemplazar dinero por capital, elevando los precios de los activos y reduciendo los tipos de interés reales. Así, el fenómeno de ilusión monetaria parcial sugiere que, aunque el efecto Fisher se manifiesta, su impacto es atenuado, lo que implica que las políticas monetarias tradicionales, basadas en el ajuste directo de las tasas de interés nominales para controlar la inflación, podrían no ser tan efectivas como se espera. Además, este hallazgo sugiere potenciales problemas en diversos aspectos que vinculan a la administración pública, como en la gestión gubernamental, la planificación fiscal y la estabilidad financiera, aspectos que se analizan detalladamente a continuación.

La administración del gobierno enfrenta desafíos cuando las tasas de interés nominales no se ajustan plenamente a la inflación. En ese sentido, investigaciones indican que una política monetaria que no ancle las expectativas adecuadamente puede provocar ineficiencias y volatilidad en los mercados financieros (Taylor, 1993). En Colombia, la parcialidad en el ajuste sugiere que el Banco de la República necesita fortalecer la comunicación de sus objetivos inflacionarios y ajustar sus herramientas para lograr una respuesta más precisa en las tasas nominales (Mishkin, 2007). Esto es fundamental para mejorar la predictibilidad del entorno macroeconómico y la eficacia de las políticas macroeconómicas aplicadas.

En términos de planificación fiscal, la subestimación del impacto inflacionario en las tasas de interés nominales puede distorsionar la gestión de la deuda pública. Tal como lo señala Fischer (1981), si las tasas de interés no reflejan adecuadamente la inflación, el costo real de la deuda puede variar, impactando negativamente las finanzas del gobierno. Esto es especialmente relevante en economías emergentes como la colombiana, donde la estabilidad fiscal depende de un control riguroso de las cuentas públicas (Blanchard y Fischer, 1989). Por tanto, es crucial implementar políticas que vinculen las proyecciones fiscales con los ajustes necesarios en las tasas de interés para minimizar el riesgo de desequilibrios.

La estabilidad financiera también se ve afectada por un ajuste incompleto de las tasas de interés. Cuando las tasas nominales no reflejan plenamente la inflación, se crea un entorno de mayor riesgo crediticio y especulación financiera (Bernanke y Gertler, 1995). En Colombia, esto podría incentivar a los agentes a tomar deuda a tasas artificialmente bajas, elevando la vulnerabilidad del sistema financiero en un contexto de inflación persistente. Las autoridades regulatorias deben entonces establecer mecanismos prudenciales, que consideren estas distorsiones para mantener la solidez del sistema y prevenir crisis sistémicas, siguiendo las recomendaciones de estudios previos sobre estabilidad macroeconómica (Schwartz, 1995).

No obstante, este aspecto requiere un análisis más profundo en futuras investigaciones. Por su parte, estos hallazgos son coherentes con la literatura existente y el análisis empírico previo. En particular, son consistentes con lo identificado por Rodríguez et al. (2021), ya que sugieren que la neutralidad del dinero no se cumple. En una economía colombiana con inflación baja y estable, esta actúa como un impuesto sobre el dinero, llevando al público a invertir en otros activos y presionando a la baja las tasas reales de interés, lo que impide que el efecto Fisher se manifieste en su totalidad.