Aprendizaje basado en juegos para la enseñanza de la probabilidad en la Administración pública

Introducción

En este artículo se presenta una estrategia enfocada en la práctica de la enseñanza de la probabilidad con estudiantes de primeros semestres de educación superior. Así mismo, se constituye como una reflexión del Laboratorio de Innovación en Administración Pública de la Escuela de Administración Pública (ESAP) sobre el procedimiento de transversalización de la innovación en los programas académicos y de extensión de la ESAP, además de ser un estudio en innovación pedagógica en administración pública. Lo anterior en el marco de desarrollo de acciones documentadas para el fortalecimiento de la innovación pedagógica en procesos formativos o de capacitación en administración pública, específicamente en torno a conceptos de probabilidad, usando un juego de mesa.

Esta investigación empezó por situar la construcción de juegos de mesa para la docencia universitaria, en el contexto de los diferentes estilos y prácticas pedagógicas, planteándola como una actividad alternativa de aprendizaje. Luego, se contextualizaron algunos de los retos de la docencia universitaria que explican el papel del juego como herramienta de innovación, haciendo énfasis en el ABJ para la enseñanza de la estadística. Finalmente, se explicó la disposición de herramientas como el inventario de conceptos de estadística, específicamente en su uso para la evaluación de la actividad lúdica.

Buscando comprender las diferencias entre los tipos de enseñanza, surgió en la literatura la posibilidad de caracterizar un estilo o forma de llevar a cabo la actividad pedagógica, el llamado estilo de enseñanza. Como discute Rendón (2013), existen diferentes definiciones. Para Camargo Uribe y Hederich Martínez (2007), los estilos de enseñanza son “las diferencias claramente identificables entre los profesores en su manera de enseñar” (p. 2); estos autores hacen especial énfasis en dos criterios, uno desde la tradición psicológica y otro desde la tradición pedagógica.

Desde el primer criterio se diferencia el estilo cognitivo analítico, asociado a un abordaje formal y detallado en el cual quien enseña tiene un control estrecho del proceso de enseñanza, del holístico, que es informal, flexible y fomenta el trabajo en equipo. En la tradición pedagógica existe una dicotomía entre prácticas tradicionales, en las que el profesor es un transmisor de conocimientos, en oposición a una práctica alternativa en la que su rol sería el de facilitar las relaciones y el aprendizaje entre quienes están aprendiendo (Camargo Uribe y Hederich Martínez, 2007).

Los autores del presente documento encuentran, en su experiencia docente, que tanto el estilo cognitivo analítico como el holístico tienen un lugar en el salón de clase, especialmente en la enseñanza de las matemáticas y la estadística, es más, se complementan. La enseñanza formal y detallada apoya la interiorización de las relaciones y conceptos que son nuevos para quien estudia, lo que solidifica las habilidades básicas cognitivas, especialmente el poder recordar los conceptos básicos. La flexibilidad y el trabajo en equipo aportan en la comprensión de los conceptos superiores y su memorización a largo plazo. Teniendo en cuenta esta descripción desde una clasificación tipológica, los juegos de mesa constituyen una práctica pedagógica alternativa asociada a un estilo pedagógico holístico.

Ahora, ¿cómo se sitúa esta práctica pedagógica en el contexto amplio de las necesidades de la enseñanza universitaria? Un elemento destacado en la discusión de la calidad de la educación es el de la llamada calidad docente. En trabajos como el de Ripoll-Nuñez y Arrieta-Caycedo (2022), el docente de calidad se define, en particular, a partir de tres características, “ser comunicador efectivo; ser competente en su disciplina; y ser respetuoso con los estudiantes” (p. 10). Este diagnóstico no es único de estos autores, dado que incluso en la experiencia propia de los autores del presente estudio en la práctica pedagógica en Colombia se suele hacer énfasis en estas tres características.

Con todo, dicho diagnóstico sobre los elementos de la calidad docente no es unánime en la literatura educativa. Por ejemplo, autores como Bowers et al. (2018) llevan a cabo un análisis más amplio del concepto de calidad en la educación. Una de sus conclusiones es que hay diferentes definiciones al respecto y no hay consenso sobre lo que significa la calidad.

Por otra parte, uno de los retos de la docencia es el del ciberplagio académico, como lo mencionan Llovera-López et al. (2023), el cual se ha visto facilitado por la introducción por parte de diferentes empresas de modelos de lenguaje que permiten construir texto sintético. En este sentido, las estrategias educativas como los juegos de mesa y otros, que hacen uso de “baja tecnología”, surgen como una alternativa a las pantallas y la automatización.

La integración de los juegos en la enseñanza de la estadística ha sido objeto de gran atención en los últimos años, ya que los educadores se esfuerzan por crear entornos de aprendizaje atractivos y eficaces. Los juegos se han utilizado ampliamente para enseñar materias como matemáticas, ciencias y lenguaje, y se ha demostrado que tienen un impacto positivo en el aprendizaje y la motivación de los estudiantes (Aguilar Fernández y Zamora Araya, 2024; Mostto y Parra, 2024; Ramlan y Fabil, 2020; Rosas Alfonzo y Cabrera Rojas, 2024).

Una de las ventajas más importantes en la incorporación de los juegos en el proceso de enseñanza-aprendizaje de la estadística es que les facilita a los alumnos el aprendizaje de esta materia. Los juegos pueden diseñarse de tal manera que los jóvenes se diviertan mientras interiorizan nociones y principios estadísticos. Este tipo de acercamiento puede ser útil en estudiantes con apatía, desinterés o discordia con respecto a la estadística, o para los que piensan que esta es compleja. Barco Rojas et al. (2024) y Molina et al. (2023) mencionan que la actitud que muestran los alumnos que abordan el aprendizaje matemático, aplicable al aprendizaje de la estadística, es un factor que define la posibilidad de aprenderlo y aplicarlo. Sin embargo, si esta materia se rechaza, se tiende a afectar la superación y las expectativas profesionales.

En un trabajo de investigación, Vu y Feinstein (2017), citados en Alper et al., 2021), mostraron que el uso de juegos en el ámbito educativo y estudiantil tiene impactos efectivos en sus calificaciones e influye favorablemente en su conducta. Esto sugiere que la incorporación de juegos en la enseñanza de la estadística puede tener un efecto tangible en los resultados de aprendizaje de los estudiantes.

En todo caso, para que los juegos sean utilizados en el aula se deben tener en mente los procesos llevados a cabo para planificarlos y facilitarlos por parte del docente. En el uso de juegos en la educación matemática en el aula, los estudiantes pueden encontrar dificultades al momento de pensar sobre los conceptos estadísticos que se están enseñando sin el respaldo del docente. Por esta razón, se necesita la participación activa de los instructores en el proceso de ABJ, pues ellos son responsables de guiar a los estudiantes en la comprensión de los conceptos y principios de la estadística, y de realizar discusiones para crear más posibilidades de aprendizaje (Hernández y Romero, 2019).

El uso de juegos como innovación pedagógica en la enseñanza de la estadística es muy favorable, pues al crear entornos de aprendizaje atractivos e interactivos, los juegos pueden ayudar a que los conceptos estadísticos sean más accesibles y amenos para los estudiantes, lo que conduce a una mejora de los resultados del aprendizaje. Sin embargo, la efectividad de tal enfoque depende de que el docente realmente pueda facilitar y presentar tareas y actividades que estén diseñadas para reforzar los conceptos fundamentales que se enseñan durante el proceso de ABJ (Ramlan y Fabil, 2020).

En el campo de la administración pública, se ha destacado la importancia de implementar nuevos métodos didácticos. En particular, la integración de juegos de simulación educativa ha surgido como un enfoque prometedor, porque estos juegos pueden ayudar a los estudiantes a comprender las ideas sobre distribuciones de probabilidades de una manera divertida y emocionante (Linehan et al., 2011), aunque el contexto de aplicación no necesariamente restrinja el diseño mismo del juego.

Existen numerosos beneficios que acompañan la adopción de juegos de simulación como parte del currículo para la práctica de la administración pública. Tales juegos pueden crear un ambiente de aprendizaje activo donde los aprendices pueden practicar el conocimiento teórico en un entorno realista y libre de riesgos, lo que mejora la comprensión y la aplicabilidad en contextos profesionales (Huo, 2019). Además, las características interactivas de estos juegos también tienen beneficios en la práctica, porque fomentan el aprendizaje de habilidades importantes como la resolución de problemas, la toma de decisiones y el trabajo en equipo, fundamentales en la práctica de la administración pública.

De acuerdo con Chen y Downing (2006), el aprendizaje profundo está asociado al uso de juegos de simulación en la enseñanza de la contabilidad de gestión, debido a que los alumnos no solo se limitan a aplicar los conceptos teóricos, sino que además ponen en juego una serie de competencias en la práctica que incluyen habilidades analíticas, interpersonales y de comunicación. Del mismo modo, en el contexto de los cursos de gestión financiera, las simulaciones empresariales han resultado ser una herramienta valiosa para facilitar el aprendizaje, ya que permiten a los estudiantes experimentar la aplicación práctica de los principios financieros en un entorno libre de riesgos (Freire-Araujo y Gallardo-Medina, 2023).

Sin embargo, se han presentado algunas dificultades de aplicación y desarrollo de los juegos de simulación en el marco de la enseñanza de la administración pública (Harguindéguy et al., 2023). Si bien la creación de una cultura de uso generalizado de los juegos de simulación por parte de los profesores puede suponer un desafío, existen medidas que pueden adoptarse para ampliar significativamente al grupo de instructores que incorporan estas opciones a sus prácticas docentes. Superando estos retos, y utilizando todo el potencial que tienen los juegos de simulación, las facultades de administración pública en sus programas de estudios podrán involucrar a los estudiantes en un proceso de aprendizaje más activo, preparándolos mejor para navegar por las complejidades del campo de la gestión pública.

Partiendo de la situación antes descrita, se reflexiona sobre cómo el ABJ (serios y de simulación) facilita los procesos de enseñanza-aprendizaje de la estadística para la administración pública. Para ello, se presenta un análisis reflexivo sobre el ABJ para la enseñanza de la probabilidad —la planificación de un juego serio—, junto con una actividad evaluativa para identificar la influencia que el juego podría tener en los estudiantes, y se finaliza con unas conclusiones sobre el ABJ como metodología activa en los procesos de enseñanza-aprendizaje. El resultado o aporte de este artículo al campo de conocimiento de la enseñanza es, justamente, una perspectiva analítica propuesta por los autores sobre el juego en particular presentado en este documento y la metodología que se plantea para ser utilizada en la evaluación de este tipo de iniciativas.

Aprendizaje basado en juegos para la enseñanza de la estadística

Existe una amplia literatura en torno al empleo de diferentes tipos de juegos tanto en la enseñanza como en la aplicación de contenidos de aprendizajes en programas de pregrado y posgrado. Al respecto, Pope (2021) e Ibáñez Usach et al. (2015) hacen referencia a los diferentes usos que se han dado en la literatura a los juegos de mesa como herramientas educativas. En Ezezika et al. (2021), se presenta un juego de tablero para la enseñanza de la salud pública en biología, mientras que Martindale y Weiss (2020) discuten una iniciativa similar para estudiar la fosilización. Por su parte, Bochennek et al. (2007) reportan el uso de juegos de cartas para la enseñanza médica. Smith y Golding (2018) llevan a cabo una revisión concienzuda de la literatura sobre los juegos de tablero en la educación. Adicionalmente, los juegos digitales (o videojuegos) han sido usados de una manera más amplia y, por ejemplo, Romero Valbuena et al. (2018) estudian cómo estos pueden complementar la enseñanza de la ingeniería industrial.

Por otro lado, el profesor Juan David García, del Departamento de Medicina de la Universidad Nacional de Colombia, y el grupo El juego como recurso del aprendizaje, han creado el juego El pirata del mar de los Vectores, dentro de la iniciativa JugatoriUN, el cual se utiliza como una herramienta para enseñar las bases de álgebra vectorial a estudiantes nuevos, al nivel posgradual (Universidad Nacional de Colombia, 2021, 1h01s).

Ahora bien, según Rodríguez y Mas y Rubí (2024), el ABJ consiste en utilizar elementos del juego en contextos educativos para obtener mejores resultados de aprendizaje. En ese sentido, la gamificación en el ámbito educativo ha mostrado tener beneficios como la retroalimentación constante, la motivación para aprender y la creación de aprendizajes más significativos y autónomos (Caicedo et al., 2020). Sin embargo, es fundamental reconocer que la gamificación por sí sola no es suficiente, sino que es necesario incorporar otros elementos que le den coherencia y la conviertan en una experiencia significativa en el contexto educativo (López y Navarro-Mateos, 2022). Como se constata, las estrategias de gamificación han demostrado ser efectivas para captar la atención de los estudiantes, desafiándolos a resolver problemas, adquirir nuevos conocimientos y aprender nuevas habilidades (Caicedo et al., 2020; Espinosa, 2016; Mateos et al., 2021).

Se ha demostrado también que la incorporación de actividades basadas en juegos en la educación estadística aumenta la participación de los estudiantes y el rendimiento académico (Leonardou et al., 2020). Además, el ABJ puede ayudar a establecer las expectativas de los estudiantes y presentar conceptos estadísticos básicos de una manera atractiva y accesible (Rastpour y Amini, 2024).

Un caso de un éxito en la implementación de esta metodología en la enseñanza de estadística es el juego Adivina la edad, donde los alumnos pueden usar conceptos estadísticos como el muestreo y la estimación, al mismo tiempo que se conectan con insights psicológicos relevantes (Rastpour y Amini, 2024). De manera similar, otros investigadores han desarrollado juegos adaptativos que incorporan modelado abierto del alumno para fomentar la motivación de los estudiantes y abordar brechas específicas de habilidades, como en relación con la multiplicación (Leonardou et al., 2020). Más allá de los juegos independientes, el ABJ también se puede implementar integrando contenido docente en juegos existentes o incluyendo juegos como parte de las lecciones regulares (Alper et al., 2021). Pero, si bien los beneficios son cada vez más evidentes, también existen consideraciones prácticas y desafíos potenciales que deben considerarse.

Ante a la falta de evidencia empírica suficiente, un análisis reciente de la literatura aborda el creciente conjunto de estudios sobre la utilización de la realidad aumentada en la enseñanza en varios entornos. Los resultados indican que es posible incrementar la participación y los logros académicos de los alumnos de manera eficaz, pero es necesario investigar más sobre las características de diseño y las estrategias de implementación para obtener resultados óptimos (Tobar-Muñoz et al., 2023).

Por otra parte, los juegos de mesa pueden ser una herramienta valiosa para enseñar estadística, en la medida en que permiten a los estudiantes participar en la aplicación práctica de conceptos estadísticos como probabilidad, valor esperado y análisis de datos. Al participar en tales juegos, los estudiantes pueden desarrollar una comprensión más profunda de estos conceptos de una manera atractiva e interactiva (Bonilla y Gutiérrez, 2024).

La adopción del ABJ para la educación estadística representa una dirección prometedora, pero es importante asegurarse de que los elementos de gamificación estén bien diseñados e integrados de una manera que respalde los objetivos de aprendizaje (Legaki et al., 2020).

Para la tarea de desarrollar el juego, se proponen dos principios fundamentales. El primero de ellos es que los juegos se incluyen para aumentar la motivación, y por tanto, deben ser divertidos. En la literatura se clasifican los motivadores en catorce categorías diferentes que, si bien no tienen que estar siempre todas presentes en todos los juegos, sí representan una guía de las características que les hacen atractivos. Siguiendo a Laine y Lindberg (2020), se toman como preponderantes las siguientes:

• El desafío, entendido como la motivación para llevar a cabo actividades que se encuentran cercanas al nivel de habilidad del participante.

• El control, que es la capacidad que tienen quienes juegan de influenciar el juego y sus eventos. En juegos de estrategia como go o Carcassonne, este control del juego consiste en la posesión del terreno que se controla. En juegos de desplazamiento de piezas como parqués, se trata de la permanencia de las piezas y de su avance en el tablero.

• La curiosidad, como el deseo de descubrir los diferentes acertijos que se presentan.

• La interacción social, en cuanto quienes participan en el juego pueden apoyarse.

El segundo principio plantea que los juegos tienen que centrarse en la pedagogía, es decir, que la lúdica no puede reñir con el aprendizaje, distrayendo del objetivo de fondo (Gros, 2017). Esto se logra diseñando una dinámica del juego que esté en línea con el juego mismo. Por ejemplo, un juego enfocado en geometría desarrolla sus reglas a través de este tipo de relaciones, como es el caso del juego Los piratas del mar de los Vectores, mencionado anteriormente.

Finalmente, el uso del ABJ para la enseñanza de la estadística no está exento de desafíos, pues se debe prestar una cuidadosa consideración al diseño y la implementación de estas actividades para asegurar que aborden eficazmente los objetivos de aprendizaje y proporcionen una retroalimentación constructiva a los estudiantes.

Planificación del aprendizaje basado en juegos

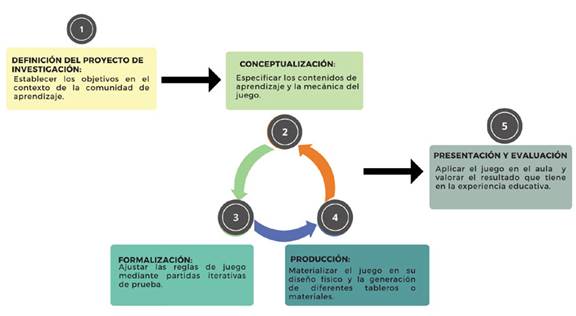
Tanto Morales Moras (2017) como Rodríguez Díaz et al. (2021) proponen que la creación de un juego que tenga como objetivo el aprendizaje, los llamados juegos serios, debe seguir una metodología dispuesta en una serie de fases. A continuación (figura 1), se presenta una adaptación en cinco fases de la metodología basada en los autores:

Figura 1: Planificación del ABJ

Fuente: adaptado de Morales Moras (2017) y Rodríguez Díaz et al. (2021).

Teniendo en cuenta lo anterior, se describe la experiencia de los autores del presente artículo en la planificación del ABJ para la enseñanza de la probabilidad:

• Definición del proyecto de investigación. Inicialmente, uno de los autores participó en actividades de divulgación de la metodología ABJ por parte de la comunidad académica de la Universidad Nacional de Colombia, en el mencionado JugatoriUN. Esto llevó a una etapa de exploración, que culminó con la especificación del objetivo general, la metodología de investigación pedagógica y la definición de la estadística como disciplina a desarrollar en el proyecto pedagógico, lo que permitió incluir el proyecto dentro de la estrategia pedagógica del Laboratorio de Innovación en Administración Pública

Las fases de conceptualización, formalización y producción se llevaron a cabo iterativamente. Una primera iteración del proceso se realizó de la siguiente forma:

• Conceptualización. Se estableció el contenido alrededor de las características de las distribuciones de probabilidad, un aspecto específico de la enseñanza de la estadística, lo que permitió diseñar unas reglas de juego que siguieran el enfoque lúdico y el enfoque pedagógico mencionados anteriormente.

• Formalización. Se procedió a una prueba piloto del juego, lo que posibilitó un ajuste de sus reglas y el enfoque en aspectos prácticos de usabilidad y avance.

• Producción. Cada partida del juego que se presenta requiere de un nuevo tablero. Para generalizar su uso, los autores escribieron y diseñaron un programa en lenguaje Phyton que permitiera la automatización de estas tareas.

El proceso de prototipado y construcción posibilitó una reflexión sobre la interacción entre las reglas de juego, los conceptos estadísticos y el producto mismo. En este caso particular, se ajustó la mecánica de juego para incluir elementos de motivación que aumentaran la interacción social, como se mencionará en la sección de descripción. Se hicieron nuevas partidas de prueba, posibilitando ajustes de formalización y producción. Finalmente, estos cambios generaron necesariamente modificaciones en cuanto a la producción de los materiales.

Presentación y evaluación. Las estrategias de presentación del juego incluyeron la socialización por parte de los autores frente a la comunidad del laboratorio, su uso ante la comunidad académica y la producción científica de un artículo. Este proceso de planificación generó una primera versión del juego, que se explica a continuación.

Descripción del juego

Nombre: El misterioso tablero de las posibilidades

Objetivo pedagógico: Comprender las distribuciones de probabilidad discreta.

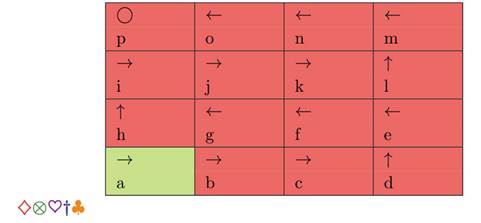
Cómo ganar: El objetivo de los participantes consiste en resolver dieciséis acertijos, cada uno de ellos relacionado con una de las casillas de un tablero. Las casillas están identificadas con letras desde la a hasta la p. La figura 2 presenta la estructura del tablero, con la dirección del desplazamiento. Inicialmente, las piezas se ubican fuera del tablero, pero se suponen contiguas a la casilla marcada como a.

Figura 2: Estructura del tablero de juego

Fuente: elaboración propia

Acertijos: Los acertijos relacionados con cada una de las casillas del tablero corresponden a una distribución de probabilidad discreta. Resolver cada acertijo significa determinar cuáles son los parámetros de la distribución. Ahora, los parámetros tienen relación con los estadísticos de centro y variabilidad, así:

• Uniforme discreta: se caracteriza por un valor mínimo y un máximo.

• Binomial: caracterizada por el número de pruebas y la probabilidad de éxito.

• Poisson: caracterizada por su promedio.

Dinámica del juego: El juego tiene dos roles, jugadores y guía. Quien tiene el rol de guía sabe la solución de los acertijos y tiene el papel de determinar si los que juegan han resuelto correctamente los acertijos. La implementación del juego que se construye y presenta en este trabajo tiene un software que genera los tableros, disponiendo de lo necesario para cada una de las partidas.

Para la organización inicial, se ponen las piezas afuera del tablero y se define un orden de acción. En el desarrollo de cada partida, cada persona que juega tiene tres opciones, pero debe elegir una sola de ellas. Estas son:

1. Pedir a quien guía la partida un valor estadístico de centro o variabilidad (promedio, desviación estándar, mediana, rango, máximo o mínimo) de una casilla contigua a donde está su pieza. En el primer turno lo puede hacer sobre la primera casilla.

2. Puede lanzar un dado de diez caras, obteniendo un número de tokens. Con uno de estos puede:

1. Mover su pieza sobre las casillas cuyo acertijo ya haya sido resuelto, es decir para las que la distribución de probabilidad ya haya sido identificada.

2. Pedir un número aleatorio correspondiente a una de las casillas contiguas. En el primer turno solo lo puede hacer con respecto a la distribución asociada a la primera casilla.

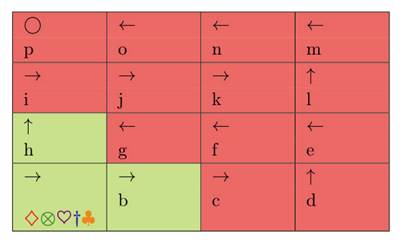
1. Si cree saber cuál es la distribución correspondiente a una casilla, puede identificarla, mencionando en voz alta los parámetros de la distribución. Las piezas de ahora en adelante podrán moverse a las casillas cuya distribución ha sido identificada. En la figura 3, se puede observar que ya se han identificado las distribuciones correspondientes a las casillas a, b y h, con el color verde, para indicar que las piezas podrían desplazarse a estas casillas.

Figura 3: Estructura del tablero de juego con distribuciones identificadas

Fuente: Elaboración propia

Para incluir la motivación por interacción social, se asigna un rol a la persona que guía, otorgándole una ficha especial, que persigue a las demás. A partir del turno 4, lanza un dado de diez caras (D10), el cual cumple las siguientes instrucciones:

1. Si obtiene 10 a partir del siguiente turno mueve la pieza.

2. Si puede mover la pieza, hace una casilla por cada dos tokens; puede avanzar en ambos sentidos.

3. Si al final del movimiento llega a la pieza de un jugador, lo puede excluir del juego.

La dinámica de esta pieza que puede dejar por fuera del juego a las demás genera una relación de cooperación entre los jugadores, lo que ayuda a su motivación.

El juego finaliza en dos escenarios: el primero, que quienes juegan averigüen todas las distribuciones y por lo tanto ganen; el segundo, que todas sus piezas sean removidas del tablero por quien guía, por lo tanto, pierden.

Planificación de evaluación de la actividad lúdica a través del inventario de conceptos de estadística

La evaluación del juego descrito implica la planeación de una actividad que identifique de forma apropiada los avances que, en materia conceptual, se generen en los involucrados en la actividad lúdica. Dado que se pretende profundizar en los conceptos concretos de distribuciones de probabilidad discreta, es importante implementar un test que tenga este mismo enfoque. Los inventarios de conceptos tienen el perfil necesitado y por tanto son apropiados como parte de la actividad evaluativa.

Los inventarios de conceptos aparecen a mediados de los ochenta aplicados a pruebas de mecánica (Halloun y Hestenes, 1985), pero posteriormente han sido extendidos a la evaluación de nuevas áreas en ciencias, matemáticas (Epstein, 2013; Steif y Dantzler, 2005) y estadística (Allen et al., 2004; Lee et al., 2023; Stone et al., 2003).

Los inventarios de conceptos de estadística (SCI por sus siglas en inglés) constituyen un acervo de preguntas que permiten configurar un test para evaluar la comprensión de temas claves de estadística (Allen, 2006). Sin embargo, no se centran en la capacidad para realizar cálculos extensos o de alto nivel técnico, sino que, por el contrario, intentan acercarse al verdadero nivel de entendimiento que tienen los estudiantes de conceptos pertenecientes a diferentes temas de la estadística.

Por ejemplo, Allen (2006) validó un test aplicado a estudiantes de diferentes carreras con veinticinco preguntas de selección múltiple, el cual comprende cuatro temáticas principales: análisis gráfico, estadística descriptiva, estadística inferencial y probabilidad. En Colombia, los inventarios de conceptos se han utilizado para evaluar el aprendizaje de las matemáticas en grupos grandes, incluyendo estudiantes del programa Ser Pilo Paga (Villalobos-Camargo, 2021), por lo que son apropiados para identificar, de manera objetiva, el valor agregado que puede generar una actividad lúdica innovadora, orientada generalmente a cimentar, a través del juego, conceptos propios de una temática. Por otro lado, los test requieren de un proceso que legitima su significancia y que normalmente comprende conceptos de validación y fiabilidad.

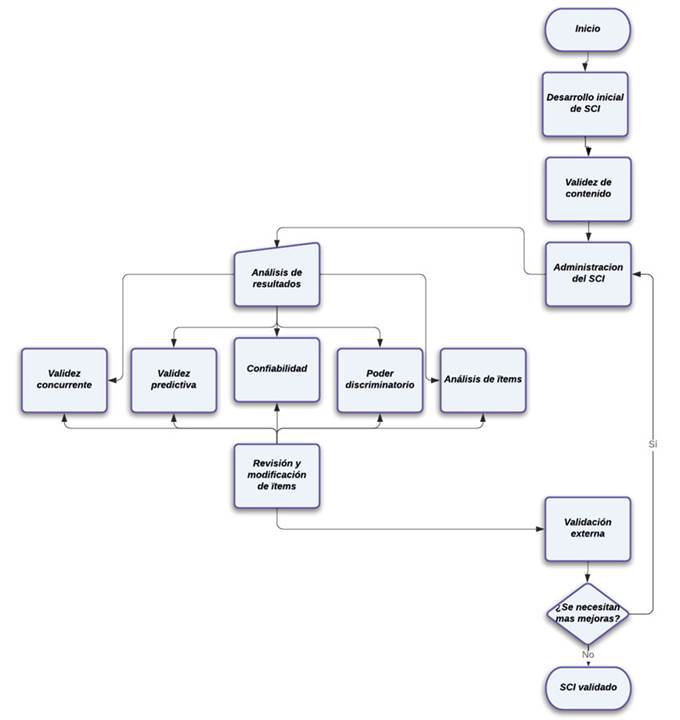
La figura 4 ilustra una posible manera de describir de forma esquemática el proceso completo que implica validar un instrumento apropiado para evaluar el afianzamiento conceptual presente luego de exponer a los estudiantes a alguna actividad pedagógica (Allen, 2006; Allen et al., 2004).

Figura 4: Esquema a usar en la validación del instrumento de evaluación

Fuente: adaptado de Allen (2006).

El inicio del proceso se enfoca en la selección de las temáticas a evaluar, seguido del desarrollo inicial de las preguntas a incluir en las pruebas. En esta primera fase de desarrollo del SCI se implementan validaciones preliminares, como uso de las preguntas en versiones online, que brinden retroalimentación inmediata. La siguiente fase, de validez de contenido, implica una nueva revisión del enfoque temático de las preguntas acompañada de la opinión de expertos, los cuales se encargarán de adiciones o correcciones de las pruebas diseñadas. Posterior a la aplicación de las pruebas, los puntajes deberán ser sometidos a validaciones adicionales asociadas a predictibilidad y confiabilidad, entre otras, que, sumado a una última revisión externa, permitirán consolidar un banco de preguntas estructuradas que brinden confianza de sus resultados.

La evaluación puede tener propósitos diagnósticos, instructivos o educativos (Mora Vargas, 2004). Esto último está relacionado con la posibilidad de asociar dicha evaluación con las actividades o metodologías usadas en el salón de clase por parte del guía o docente. En particular, el inventario de conceptos ha sido implementado en experimentos del tipo pre y post-test, donde se mostró una correlación entre los resultados obtenidos con las metodologías implementadas en clase (Hake, 1998). Esto implica la posibilidad de acercarse, al menos de forma preliminar, al impacto que una actividad o metodología podría tener en la apropiación conceptual de algún tema particular.

En términos de Cook y Campbell (1976), el diseño experimental que podría usarse sería:

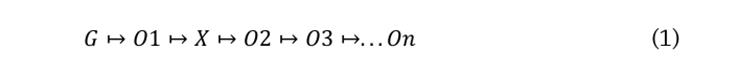
En donde G representa el grupo al que se expone a la actividad pedagógica, O representa los resultados obtenidos del pre test y post-test y X está asociada a la intervención pedagógica.

En este caso particular se tendrán solo dos resultados pre y post-test, los cuales podrían ser comparados para, de esta forma, detectar la posible influencia causada por la actividad lúdica implementada. Para expresar de forma cuantitativa la ganancia que se obtendría a causa de la actividad realizada, es posible usar el factor de Hake, comúnmente llamado también factor de ganancia (Hake, 1998), el cual ha sido ampliamente usado en diferentes estudios del tipo pre y post-test. Sin embargo, algunos autores han criticado su uso, argumentando correlaciones entre el test a priori y el factor de ganancia, lo que aumenta la posibilidad de malinterpretar la eficacia de las actividades pedagógicas implementadas (Nissen et al., 2018). Por otra parte, estas afirmaciones han sido debatidas por Coletta y Steinert (2020), quienes a partir del análisis de varias pruebas con cientos de datos concluyen que el sesgo mencionado es generado por omisión de variables y que, por lo tanto, el factor de Hake debería seguirse implementando. En término matemáticos, el factor se expresa como:

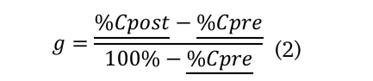
Esta expresión pretende medir el porcentaje de ganancia de aprendizaje de un conjunto de estudiantes pertenecientes a una clase. El factor se convierte así en una herramienta que permite identificar el posible valor agregado, a nivel conceptual, que los estudiantes ganen al participar en la sesión de juego. En general, este indicador es de fácil uso e interpretación, pero no tiene en cuenta la significancia estadística, y por lo tanto no puede distinguir si las diferencias entre las pruebas pre y post puedan ser a causa del azar. Para superar esta limitación, es posible tomar los resultados de las pruebas como datos pareados y calcular la diferencia entre medias a un nivel de significancia determinado.

A continuación, se presenta un ejemplo de aplicación de un inventario de conceptos sobre las distribuciones de probabilidad (uniforme discreta, binomial y Poisson), en el contexto de la administración pública, que permitiría evaluar el impacto de la actividad lúdica en la comprensión conceptual e identificar áreas de fortaleza y oportunidad sobre estos temas clave para la toma de decisiones en administración pública. Este diseño presenta dos fases:

1. Diseño del inventario: Se definen los conceptos correspondientes sobre las distribuciones de probabilidad.

• Distribución uniforme discreta: definición y propiedades; aplicaciones en la administración pública (por ejemplo, modelar la llegada aleatoria de ciudadanos a una oficina gubernamental).

• Distribución binomial: definición y propiedades; aplicaciones en la administración pública (por ejemplo, modelado de resultados de éxito/fracaso para programas gubernamentales).

• Distribución de Poisson: definición y propiedades; aplicaciones en la administración pública (por ejemplo, modelado de eventos raros como quejas ciudadanas o auditorías gubernamentales).

El inventario podría incluir preguntas de opción múltiple, verdadero/falso, y de respuesta corta, que prueben la comprensión conceptual de los estudiantes sobre las características y aplicaciones clave de estas distribuciones de probabilidad.

Preguntas de ejemplo:

• ¿Qué distribución modela el número de éxitos en un número fijo de ensayos independientes con una probabilidad de éxito constante?

1. a) Discreta uniforme

2. b) Binomial

3. c) Poisson

• Verdadero o falso: La distribución de Poisson es apropiada para modelar eventos que ocurren continuamente en el tiempo o el espacio.

• Describa un escenario de administración pública del mundo real donde se podría aplicar la distribución discreta uniforme.

Aquí, se aplicaría la fórmula de Cook y Campbell (1976) en el diseño experimental para encontrar una correlación entre los resultados obtenidos con las metodologías implementadas en clase.

• Grupo (G): Estudiantes de un programa de administración pública.

• Pre-test (O1): Evaluar comprensión inicial de los conceptos clave de las tres distribuciones.

• Intervención (X): Sesión pedagógica de actividad lúdica sobre estas distribuciones.

• Post-test (O2): Evaluar comprensión posterior a la intervención.

En este sentido, la prueba previa establecería una comprensión básica, la actividad lúdica proporcionaría instrucción y la prueba posterior mediría el cambio en el conocimiento conceptual de los estudiantes.

Análisis de resultados:

Las actividades a realizar en esta fase son:

• Calcular el factor de Hake (g) para cuantificar la ganancia de aprendizaje.

• Realizar prueba estadística de diferencia de medias pareadas para determinar si los cambios son significativos.

La metodología de pre y post-test propuesta podría evaluar cómo la dinámica del juego mejora la comprensión de estos conceptos probabilísticos. En síntesis, la implementación del juego El misterioso tablero de las posibilidades en el contexto de la administración pública representa una innovadora aproximación al aprendizaje de las distribuciones de probabilidad discretas, particularmente relevante para la gestión de servicios gubernamentales, toda vez que el tablero con sus 16 casillas (a-p) y sus tres tipos de distribuciones (uniforme discreta, binomial y Poisson) se alinea perfectamente con los escenarios reales de atención ciudadana.

Discusión

La incorporación de juegos en la enseñanza de la estadística, particularmente en el ámbito de la educación superior y la administración pública, ofrece un abanico de oportunidades para mejorar el proceso de aprendizaje. En el juego que se presenta en este trabajo se pueden observar dos efectos pedagógicos. Por un lado, las sesiones en las que se incluyó el mismo se constituyeron en una práctica pedagógica holística, aumentando el interés y la motivación de los estudiantes. Por otro lado, dado que dentro de la dinámica de juego se requería determinar los parámetros de una distribución de probabilidad según la información disponible de los datos relacionados con dicha variable, se lograba una aplicación real de los conceptos de probabilidad para solucionar un problema que puede surgir en la práctica profesional. Además, con el juego se fomenta el desarrollo de habilidades complementarias, como la resolución de problemas y el trabajo en equipo, aspectos cruciales en el campo de la administración pública, en el que la toma de decisiones basada en datos es fundamental.

Más aún, El misterioso tablero de las posibilidades permite fortalecer habilidades blandas o de negociación entre quienes participan, aspecto importante que se relaciona con la administración pública. Dado que al construir el juego se tuvieron en cuenta los principios de curiosidad e interacción social, el objetivo interno del mismo —resolver todos los acertijos relacionados con las distribuciones de probabilidad— suele generar una dinámica colaborativa.

Los temas de estadística que se tratan en este juego usualmente hacen parte del ciclo básico de formación en las instituciones de educación superior. Esto lleva a que durante su desarrollo no se tengan en cuenta aspectos avanzados de la disciplina de administración pública. Sin embargo, a futuro esperamos desarrollar otros juegos enfocados en diferentes aspectos, como son temas de carácter territorial o presupuestal.

La dinámica cooperativa del juego, donde los participantes deben colaborar para evitar ser eliminados por la ficha especial del guía, es análoga a las relaciones que ocurren en un ambiente de trabajo en equipo, necesario en las oficinas gubernamentales. Los tres tipos de acciones disponibles para los jugadores (solicitar estadísticos, usar tokens para movimientos o identificar distribuciones) asemejan a las decisiones que los funcionarios públicos deben tomar en la gestión de recursos y servicios. Esta forma de gamificación no solo incrementa el entendimiento teórico, sino que también fortalece habilidades prácticas en la toma de decisiones fundamentadas en datos, tal como se refleja en el juego al analizar datos estadísticos para identificar distribuciones adecuadas, de forma similar a como se deben analizar patrones de atención al cliente en contextos reales para mejorar la calidad de los servicios que se ofrecen en las oficinas gubernamentales.

No obstante, la ejecución exitosa de estos juegos educativos enfrenta desafíos. Necesita de una cuidadosa planificación de los maestros, quienes deben encontrar un equilibrio entre las estrategias divertidas y el enfoque analítico-cognitivo en la enseñanza. La presencia activa del profesor es crucial para dirigir el proceso de aprendizaje y garantizar la correcta comprensión de los conceptos estadísticos. Además, es importante abordar desafíos (como lograr la aceptación de los profesores) y crear formas eficaces de evaluar el impacto de los juegos en el aprendizaje.

Un punto adicional está asociado a la evaluación de la actividad lúdica. La formulación, el desarrollo y la validación de las herramientas apropiadas para un acercamiento oportuno a los avances en la compresión conceptual de los temas centrales asociados a la actividad, en el presente caso de distribuciones discretas, constituyen en sí mismas un proceso dispendioso que no está exento de complejidades. Sin embargo, a partir de la evaluación se puede hacer un diagnóstico formal que revele posibles oportunidades de mejora, no solo en el diseño del juego sino de la actividad general presentada en el salón de clase, en la medida en que diversos factores pueden influir en el enfoque o la disposición del grupo.

En consecuencia, a pesar de que el ABJ tiene un gran potencial para transformar la enseñanza de la estadística en la educación superior y la administración pública, su éxito está condicionado a un enfoque cuidadoso y equilibrado. Los maestros tienen que pensar detenidamente en la incorporación de estos juegos en sus planes de estudio actuales, en cómo fomentar de manera efectiva el aprendizaje a través de ellos y en cómo evaluar su efecto en la comprensión y retención de conceptos probabilísticos por parte de los alumnos. Al hacer uso de esta técnica novedosa, los individuos pueden obtener beneficios y al mismo tiempo reducir los posibles obstáculos, lo cual configura un ambiente de aprendizaje más eficaz y dinámico.